
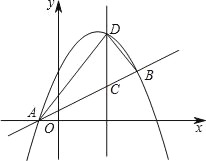
【题目】如图,抛物线y=ax2+bx+![]() 与直线AB交于点A(﹣1,0),B(4,
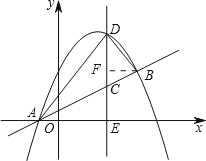
与直线AB交于点A(﹣1,0),B(4,![]() ),点D是抛物线A、B两点间部分上的一个动点(不与点A、B重合),直线CD与y轴平行,交直线AB于点C,连接AD,BD.
),点D是抛物线A、B两点间部分上的一个动点(不与点A、B重合),直线CD与y轴平行,交直线AB于点C,连接AD,BD.
(1)求抛物线的表达式;
(2)设点D的横坐标为m,△ADB的面积为S,求S关于m的函数关系式,并求出当S取最大值时的点C的坐标.
【答案】(1)y=﹣![]() x2+2x+
x2+2x+![]() (2) C(
(2) C(![]() ,
,![]() )
)
【解析】分析: (1)将点A、B的坐标代入抛物线的解析式,求得a、b的值,从而得到抛物线的解析式;
(2)设直线AB为:y=kx+b.将A、B的坐标代入可得到k,b的方程组,从而可求得k,b于是得到直线AB的解析式,记CD与x轴的交点坐标为E.过点B作BF⊥DC,垂足为F.设D(m,﹣![]() m2+2m+
m2+2m+![]() )则C(m,
)则C(m,![]() m+
m+![]() ),依据三角形的面积公式可得到S与m的函数关系式,接下来由抛物线的对称轴方程,可求得m的值,于是可得到点C的坐标.
),依据三角形的面积公式可得到S与m的函数关系式,接下来由抛物线的对称轴方程,可求得m的值,于是可得到点C的坐标.
详解:
(1)∵由题意得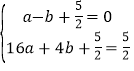 ,解得:
,解得: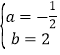 ,
,
∴y=﹣![]() x2+2x+
x2+2x+![]() .
.
(2)设直线AB为:y=kx+b.则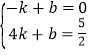 ,解得
,解得![]()
直线AB的解析式为y=![]() +
+![]() .
.
如图所示:记CD与x轴的交点坐标为E.过点B作BF⊥DC,垂足为F.
设D(m,﹣![]() m2+2m+
m2+2m+![]() )则C(m,
)则C(m,![]() m+
m+![]() ).
).
∵CD=(﹣![]() m2+2m+
m2+2m+![]() )﹣(
)﹣(![]() m+
m+![]() )=
)=![]() m2+
m2+![]() m+2,
m+2,
∴S=![]() AEDC+
AEDC+![]() CDBF=
CDBF=![]() CD(AE+BF)=
CD(AE+BF)=![]() DC=
DC=![]() m2+
m2+![]() m+5.
m+5.
∴S=![]() m2+
m2+![]() m+5.
m+5.
∵﹣![]() <0,
<0,
∴当m=![]() 时,S有最大值.
时,S有最大值.
∴当m=![]() 时,
时,![]() m+
m+![]() =
=![]() ×
×![]() +
+![]() =
=![]() .
.
∴点C(![]() ,
,![]() ).
).
点睛: 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求一次函数、二次函数的解析式、三角形的面积公式、二次函数的性质,用含m的式子表示出CD的长,从而得到S与m的关系式是解题的关键.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BC的垂直平分线交AC于点E,交BC于点D,且AD=AB,连接BE交AD于点F,下列结论:( )
①∠EBC=∠C;②△EAF∽△EBA;③BF=3EF;④∠DEF=∠DAE,其中结论正确的个数有

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题一:如图1,已知AC=160km,甲,乙两人分别从相距30km的A,B两地同时出发到C地,若甲的速度为80km/h,乙的速度为60km/h,设乙行驶时间为x(h), 两车之间距离为y(km).
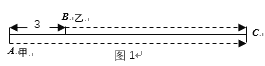
(1)当甲追上乙时,x= .
(2)请用x的代数式表示y.
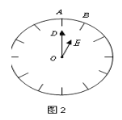
问题二:如图2,若将上述线段AC弯曲后视作钟表外围的一部分,线段AB正好对应钟表上的弧AB(1小时的间隔),易知∠AOB=30°.
(1)分针OD指向圆周上的点的速度为每分钟转动 km;时针OE指向圆周上的点的速度为每分钟转动 km.
(2)若从2:00起计时,求几分钟后分针与时针第一次重合?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上有三点 A,B,C ,若用 AB 表示 A,B 两点的距离,AC 表示 A ,C 两点的 距离,且 BC 2 AB ,点 A 、点C 对应的数分别是a 、c ,且| a 20 | | c 10 | 0 .
![]()
(1)若点 P,Q 分别从 A,C 两点同时出发向右运动,速度分别为 2 个单位长度/秒、5个单位长度/ 秒,则运动了多少秒时,Q 到 B 的距离与 P 到 B 的距离相等?
(2)若点 P ,Q 仍然以(1)中的速度分别从 A ,C 两点同时出发向右运动,2 秒后,动点 R 从 A点出发向左运动,点 R 的速度为1个单位长度/秒,点 M 为线段 PR 的中点,点 N为线段 RQ的中点,点R运动了x 秒时恰好满足 MN AQ 25,请直接写出x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,点E,F分别是边BC,AB上的点,且CE=BF.连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC.
(1)请判断:FG与CE的关系是___;
(2)如图2,若点E,F分别是边CB,BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请作出判断并给予证明;
(3)如图3,若点E,F分别是边BC,AB延长线上的点,其它条件不变,(1)中结论是否仍然成立?请直接写出你的判断.

查看答案和解析>>
科目:初中数学 来源: 题型:
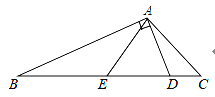
【题目】如图,在△ABC中,∠C=2∠B,点D为BC上一点,且AD⊥AB,点E是BD的中点,连接AE,且AE=DE.
(1)求证:∠AEC=∠C;
(2)若AE=8.5,AD=8,求△ABE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
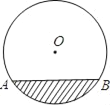
【题目】某居民小区的一处圆柱形的输水管道破裂,维修人员为更换管道,需要确定管道圆形截面的半径.如图,若这个输水管道有水部分的水面宽AB=16cm,水最深的地方的高度为4cm,求这个圆形截面的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用方程解答下列问题
(1)一件工作,甲单独做20小时完成,乙单独做12小时完成,现在先由甲单独做4小时,余下的由甲乙一起完成余下的部分需要几小时完成?
(2)王强参加了一场3000米的赛跑,他以6米/秒的速度跑了一段路程,又以4米/秒的速度跑完了其余的路程,一共花了10分钟,王强以6米秒的速度跑了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图是昌平区2019年1月份每天的最低和最高气温,观察此图,下列说法正确的是( )

A.在1月份中,最高气温为10℃,最低气温为-2℃
B.在10号至16号的气温中,每天温差最小为7℃
C.每天的最高气温均高于0℃,最低气温均低于0℃
D.每天的最高气温与最低气温都是具有相反意义的量
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com