
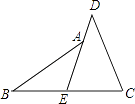
【题目】阅读下面的题目及分析过程,并按要求进行证明. 已知:如图,E是BC的中点,点A在DE上,且∠BAE=∠CDE.
求证:AB=CD.
分析:证明两条线段相等,常用的一般方法是应用全等三角形或等腰三角形的判定和性质,观察本题中要证明的两条线段,它们不在同一个三角形中,且它们分别所在的两个三角形也不全等.因此,要证AB=CD,必须添加适当的辅助线,构造全等三角形或等腰三角形.
现给出如下三种添加辅助线的方法,请任意选择其中一种,对原题进行证明.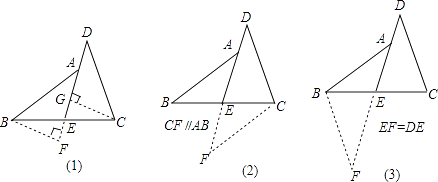
【答案】证明:方法一:作BF⊥DE于点F,CG⊥DE于点G.
∴∠F=∠CGE=90°.
又∵∠BEF=∠CEG,BE=CE,
∴△BFE≌△CGE.
∴BF=CG.
在△ABF和△DCG中,∵∠F=∠DGC=90°,∠BAE=∠CDE,BF=CG,
∴△ABF≌△DCG.
∴AB=CD.
方法二:作CF∥AB,交DE的延长线于点F.
∴∠F=∠BAE.
又∵∠ABE=∠D,
∴∠F=∠D.
∴CF=CD.
∵∠F=∠BAE,∠AEB=∠FEC,BE=CE,
∴△ABE≌△FCE.
∴AB=CF.
∴AB=CD.
方法三:延长DE至点F,使EF=DE.
又∵BE=CE,∠BEF=∠CED,
∴△BEF≌△CED.
∴BF=CD,∠D=∠F.
又∵∠BAE=∠D,
∴∠BAE=∠F.
∴AB=BF.
∴AB=CD.
【解析】证明两条线段相等,常用的一般方法是应用全等三角形或等腰三角形的判定和性质,观察本题中要证明的两条线段,它们不在同一个三角形中,且它们分别所在的两个三角形也不全等.因此,要证AB=CD,必须添加适当的辅助线,构造全等三角形或等腰三角形.


科目:初中数学 来源: 题型:
【题目】阅读材料:求1+2+22+23+24+…+22013的值.
解:设S=1+2+22+23+24+…+22012+22013,将等式两边同时乘以2得:
2S=2+22+23+24+25+…+22013+22014
将下式减去上式得2S﹣S=22014﹣1
即S=22014﹣1
即1+2+22+23+24+…+22013=22014﹣1
请你仿照此法计算:
(1)1+2+22+23+24+…+210
(2)1+3+32+33+34+…+3n(其中n为正整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2-2x-3与x轴交于A、B两点.
(1)当0<x<3时,求y的取值范围;
(2)点P为抛物线上一点,若S△PAB=10,求出此时点P的坐标.

五、解答题(本大题3小题,每小题9分,共27分)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商店运来120台洗衣机,每台售价是440元,每售出一台可以得到售价15%的利润,其中两台有些破损,按售价打八折出售。这批洗衣机售完后实得利润为_________元;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4)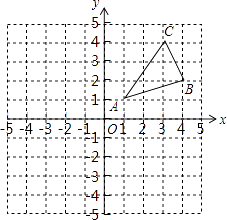
(1)请画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1;
(2)请画出△ABC关于原点O成中心对称的图形△A2B2C2;
(3)在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
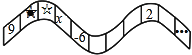
【题目】如图,从左边第一个格子开始向右数,在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.
(![]() )可求得
)可求得![]() __________,第
__________,第![]() 个格子中的数为__________.
个格子中的数为__________.
(![]() )判断:前
)判断:前![]() 个格子中所填整数之和是否可能为
个格子中所填整数之和是否可能为![]() ?若能,求出
?若能,求出![]() 的值,若不能,请说明理由.
的值,若不能,请说明理由.
(![]() )若取前
)若取前![]() 格子中的任意两个数记作
格子中的任意两个数记作![]() 、
、![]() ,且
,且![]() ,那么所有的
,那么所有的![]() 的和可以通过计算
的和可以通过计算![]() 得到,其结果为__________;若
得到,其结果为__________;若![]() 、
、![]() 为前
为前![]() 格子中的任意两个数记作
格子中的任意两个数记作![]() 、
、![]() ,且
,且![]() ,则所有的
,则所有的![]() 的和为__________.
的和为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com