
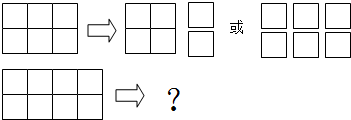
���� ��1��һ��5��2�ľ������ٿɷֳ�4�������Σ����ɷֳ�10�������Σ�
��2��һ��7��2�ľ������ٿɷֳ�5�������Σ����ɷֳ�14�������Σ�
��3��������������ҳ����еĹ��ɣ�Ȼ���ú���ĸn��ʽ�ӱ�ʾ��һ���ɼ��ɣ�
��� �⣺��1��һ��5��2�ľ������ٿɷֳ�4�������Σ����ɷֳ�10�������Σ�
��2��һ��7��2�ľ������ٿɷֳ�5�������Σ����ɷֳ�14�������Σ�
��3����һ��ͼ�Σ���һ��3��2�ľ��Σ����ٿɷֳ�1+2�������Σ����ɷֳ�1��4+2�������Σ�
�ڶ���ͼ�Σ���һ��5��2�ľ��Σ����ٿɷֳ�2+2�������Σ����ɷֳ�2��4+2�������Σ�
������ͼ�Σ���һ��7��2�ľ��Σ����ٿɷֳ�3+2�������Σ����ɷֳ�3��4+2�������Σ�
��
��n��ͼ�Σ���һ����2n+1����2�ľ��Σ����ɷֳ�n��4+2=4n+2�������Σ����ٿɷֳ�n+2�������Σ�
�ʴ�Ϊ����1��10��4����2��14��5����3��4n+2��n+2��
���� ������Ҫ�������̽��ͼ�εı仯���ɣ��ҳ�ͼ�εı仯�����ǽ���Ĺؼ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
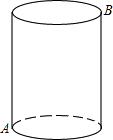 ��ͼ��һ���иǵ�Բ�����ǹޣ�һ��ɰ�������˵�B��λ�ã�һֻ���ϸպ���Բ����A����������Ե�ɰ�ǣ���ô�����������ǹޱ���������塢�����壬��������ô��������ɰ��û�е���B�������������ܵ����������λ�ã����������һ����
��ͼ��һ���иǵ�Բ�����ǹޣ�һ��ɰ�������˵�B��λ�ã�һֻ���ϸպ���Բ����A����������Ե�ɰ�ǣ���ô�����������ǹޱ���������塢�����壬��������ô��������ɰ��û�е���B�������������ܵ����������λ�ã����������һ�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����E��y���ϣ���E��x�ύ�ڵ�A��B����y�ύ�ڵ�C��D����C��0��16����D��0��-4�������߶�AB�ij���Ϊ��������
��ͼ����E��y���ϣ���E��x�ύ�ڵ�A��B����y�ύ�ڵ�C��D����C��0��16����D��0��-4�������߶�AB�ij���Ϊ��������| A�� | 10 | B�� | 8 | C�� | 20 | D�� | 16 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪A��F��E��C��ͬһֱ���ϣ�AB��CD����1=��2��AF=CE��
��ͼ����֪A��F��E��C��ͬһֱ���ϣ�AB��CD����1=��2��AF=CE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
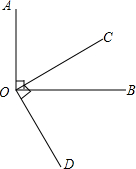 ��ͼ��OA��OB�ڵ�O��OC��OD�ڵ�O����֤����AOC=��BOD��Ҫ��д��ÿһ�����������ݣ�
��ͼ��OA��OB�ڵ�O��OC��OD�ڵ�O����֤����AOC=��BOD��Ҫ��д��ÿһ�����������ݣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com