
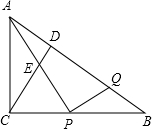
 如图,Rt△ABC中,CD为斜边AB上的高,P为BC边上一点(不与B、C重合),过点P作PQ⊥AP交AB于Q,连接AP交CD于点E.
如图,Rt△ABC中,CD为斜边AB上的高,P为BC边上一点(不与B、C重合),过点P作PQ⊥AP交AB于Q,连接AP交CD于点E.分析 (1)只要证明∠ACE=∠B,∠BPQ=∠CAE即可解决问题.
(2)过点A作AK∥BC交CD的延长线于点K.先证明△ACK∽△CBA得$\frac{AK}{AC}$=$\frac{AC}{BC}$,推出AK=$\frac{9}{2}$,由△CPE∽△KAE,得到$\frac{CP}{AK}$=$\frac{EP}{EA}$=$\frac{2x}{9}$,推出EP=$\frac{2x}{9}$EA,由△ACE∽△BPQ,得$\frac{AE}{PQ}$=$\frac{AC}{PB}$=$\frac{6}{8-x}$,由$\frac{PE}{PQ}$=y,推出y=$\frac{\frac{2x}{9}EA}{PQ}$=$\frac{2x}{9}$$•\frac{EA}{PQ}$=$\frac{2x}{9}$•$\frac{6}{8-x}$=$\frac{4x}{24-3x}$即可解决问题.
(3)分三种情形讨论:①当CE=PE=x时,②当CE=CP=x时,③当CP=EP时,∠CEP=∠DCB,分别求解即可.
解答 (1)证明:∵CD⊥AB,∠ACB=90°,
∴∠CAD+∠ACE=90°,∠B+∠CAD=90°,
∴∠ACE=∠B,
∵AP⊥PQ,
∴∠BPQ+∠APC=90°,
∵∠ACB=90°,
∴∠CAE+∠APC=90°,
∴∠BPQ=∠CAE,
∴△ABF∽△ECG.
(2)解:过点A作AK∥BC交CD的延长线于点K.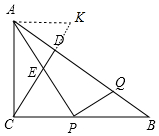
∵∠ACD=∠B,∠CAK=∠ACB=90°,
∴△ACK∽△CBA,
∴$\frac{AK}{AC}$=$\frac{AC}{BC}$,
∴$\frac{AK}{6}$=$\frac{6}{8}$,
∴AK=$\frac{9}{2}$,
∵AK∥BC,∵CP=x,
∴△CPE∽△KAE,
∴$\frac{CP}{AK}$=$\frac{EP}{EA}$=$\frac{2x}{9}$,
∴EP=$\frac{2x}{9}$EA,
∵△ACE∽△BPQ,
∴$\frac{AE}{PQ}$=$\frac{AC}{PB}$=$\frac{6}{8-x}$,
∵$\frac{PE}{PQ}$=y,
∴y=$\frac{\frac{2x}{9}EA}{PQ}$=$\frac{2x}{9}$$•\frac{EA}{PQ}$=$\frac{2x}{9}$•$\frac{6}{8-x}$=$\frac{4x}{24-3x}$,
即y=$\frac{4x}{24-3x}$.
(3)解:①当CE=PE=x时,
∵$\frac{PE}{PQ}$=y,
∴$\frac{CE}{PQ}$=y=$\frac{4x}{24-3x}$,
∵△ACE∽△BPQ,
∴$\frac{CE}{PQ}$=$\frac{AC}{BP}$,
∴$\frac{4x}{24-3x}$=$\frac{6}{8-x}$,
解得x=$\frac{9}{2}$.
②当CE=CP=x时,在Rt△ACB中,AC=6,BC=8,
∴AB=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵CE=CP,
∴∠CEP=∠CPE,
∵∠CEP=∠ACD+∠CAE,∠CPE=∠B+∠PAB,
∵∠ACD=∠B,
∴∠CAE=∠PAB,
∴△AEC∽△APB,
∴$\frac{CE}{BP}$=$\frac{AC}{AB}$,
即$\frac{x}{8-x}$=$\frac{6}{10}$,
解得x=3.
③当CP=EP时,∠CEP=∠DCB,
∵∠CEP=∠CAE+∠ACD,∠DCB=∠CAD=∠CAE+∠PAB,
∴∠ACD=∠PAB,
∵∠ACD=∠B,
∴∠PAB=∠B,
∴AP=BP=8-x,
在Rt△ACP中,AC2+PC2=AP2,
∴62+x2=(8-x)2,
解得x=$\frac{7}{4}$,
综上所述,当△CPE是等腰三角形时,CP的长为3或$\frac{9}{2}$或$\frac{7}{4}$.
点评 本题考查相似三角形综合题、勾股定理、等角的余角相等等知识,解题的关键是学会添加辅助线,构造相似三角形解决问题,学会利用参数构建方程解决问题,属于中考压轴题.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在边长为1的正方形网格中,△ABC的顶点均在格点上,点A、B的坐标分别是A(4,3)、B(4,1),把△ABC绕点C逆时针旋转90°后得到△A1B1C.
如图,在边长为1的正方形网格中,△ABC的顶点均在格点上,点A、B的坐标分别是A(4,3)、B(4,1),把△ABC绕点C逆时针旋转90°后得到△A1B1C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
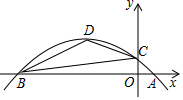 二次函数y=ax2+bx+c 的图象与x轴交于A(1,0),B两点,与y轴交于点C,其顶点D的坐标为(-3,2).
二次函数y=ax2+bx+c 的图象与x轴交于A(1,0),B两点,与y轴交于点C,其顶点D的坐标为(-3,2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com