
【题目】规定:如果一个三角形的三个角分别等于另一个三角形的三个角,那么称这两个三角形互为“等角三角形”.从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原来三角形是“等角三角形”,我们把这条线段叫做这个三角形的“等角分割线”.

(1)如图1,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,请写出图中两对“等角三角形”.
(2)如图2,在△ABC中,CD为角平分线,∠A=40°,∠B=60°。求证:CD为△ABC的等角分割线.
(3)在△ABC中,∠A=42°,CD是△ABC的等角分割线,若△ACD是等腰三角形,请直接写出∠ACB的度数.
【答案】(1)△ABC与△ACD,△ABC与△BCD等;(2)见解析;(3)84°或111°
【解析】
(1)结合题意,由三角形内角和定理,根据“等角三角形”的定义解答;
(2)根据三角形内角和定理求出∠ACB,根据角平分线的定义得到∠ACD=∠DCB=![]() ∠ACB=40°,根据“等角三角形”的定义证明;
∠ACB=40°,根据“等角三角形”的定义证明;
(3)分△ACD是等腰三角形,DA=DC、DA=AC和△BCD是等腰三角形,DB=BC、DC=BD四种情况,根据等腰三角形的性质、三角形内角和定理计算.
解:(1)因为∠A=∠A,∠ACB=∠ADC,根据三角形内角和可得∠ACD=∠B,故△ABC与△ACD是“等角三角形”; 因为∠B=∠B,∠ACB=∠BDC,根据三角形内角和可得∠DCB=∠A,故△ABC与△BCD是“等角三角形”; 因为∠ACD=∠B,∠ADC=∠BDC,∠DCB=∠A,故△ACD与△BCD是“等角三角形”.
(2)∵在△ABC中,∠A=40°,∠B=60°
∴∠ACB=180°﹣∠A﹣∠B=80°
∵CD为角平分线,
∴∠ACD=∠DCB=![]() ∠ACB=40°,
∠ACB=40°,
∴∠ACD=∠A,∠DCB=∠A,∴CD=DA,
∵在△DBC中,∠DCB=40°,∠B=60°,
∴∠BDC=180°﹣∠DCB﹣∠B=80°,
∴∠BDC=∠ACB,
∵CD=DA,∠BDC=∠ACB,∠DCB=∠A,∠B=∠B,
∴CD为△ABC的等角分割线;
(3)有三种情况.①当DA=DC时,∠ACD=∠A=42°,
∴∠ACB=∠BDC=42°+42°=84°,
②当DA=AC时,∠ACD=∠ADC=69°,
∠BCD=∠A=42°,
∴∠ACB=69°+42°=111°,
③当AC=DC时,∠ADC=∠A=42°,
∴∠BDC=180°-42°=138°=∠ACB,
此时∠B=180°-42°-138°=0°,舍去.
∴∠ACB的度数为84°或111°.


科目:初中数学 来源: 题型:
【题目】如图,△ABC是⊙O的内接三角形,AB=AC,∠BCA=65°,作CD∥AB,并与○O相交于点D,连接BD,则∠DBC的大小为

A. 15° B. 35° C. 25° D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知点D,E,F分别为BC,AD,AE的中点,且S△ABC=4cm2,则阴影部分面积S=( )cm2.
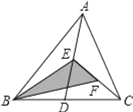
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC中,AB=AC=6,∠A=45°,点D在AC上,点E在BD上,且△ABD、△CDE、△BCE均为等腰三角形.

(1)求∠EBC的度数;
(2)求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现,销售量y(件)与销售单价x(元)符合一次函数y=kx+b,且x=65时,y=55;x=75时,y=45.
(1)求一次函数y=kx+b的表达式;
(2)若该商场获得利润为W元,试写出利润W与销售单价x之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 中,
中,![]() .设
.设![]() 的面积为
的面积为![]() .
.

①图1中,![]() 为
为![]() 中点,
中点,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 上的四点;
上的四点;
②图2中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 交于点
交于点![]() ;
;
③图3中,![]() ,D为
,D为![]() 中点,
中点,![]() .
.
其中,阴影部分面积为![]() 的是______(填序号).
的是______(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
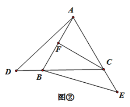
【题目】如图,△ABC是等边三角形,点D、E分别是直线BC、AC上的点,且BD=CE.
(1)如图①,当点D、E分别在线段BC、AC上时,BE与AD相交于点F.求∠AFB的度数.
(2)如图②,当点D在CB的延长线上,点E在AC的延长线上时,CF为△ABC的高线则线段CD、AF、CE、之间的数量关系是 ,并加以证明.
(3)在①的条件下,连接FC,如图③,若∠DFC=90°,AF= 3![]() ,求BF的长.
,求BF的长.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com