(1)证明:令y=0,则x
2+(a-2)x-2a=0
△=(a-2)
2+8a=(a+2)
2∵a>0,
∴a+2>0
∴△>0
∴方程x
2+(a-2)x-2a=0有两个不相等的实数根;
∴抛物线与x轴有两个交点
(2)①令y=0,则x
2+(a-2)x-2a=0,
解方程,得x
1=2,x
2=-a
∵A在B左侧,且a>0,
∴抛物线与x轴的两个交点为A(-a,0),B(2,0).
∵抛物线与y轴的交点为C,
∴C(0,-2a)
∴AO=a,CO=2a;
在Rt△AOC中,
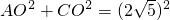
,a
2+(2a)
2=20,
可得a=±2;
∵a>0,
∴a=2
∴抛物线的解析式为y=x
2-4;
②依题意,可得直线l'的解析式为y=3x+t,A'(t-2,0),B'(t+2,0),A'B'=AB=4
∵△A'B'P为以A'B'为直角边的等腰直角三角形,
∴当∠PA'B'=90°时,点P的坐标为(t-2,4)或(t-2,-4)
∴|3(t-2)+t|=4
解得

或
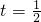
当∠PB'A'=90°时,点P的坐标为(t+2,4)或(t+2,-4)
∴|3(t+2)+t|=4
解得

或

(不合题意,舍去)
综上所述,

或
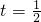
.
分析:(1)令抛物线的y值等于0,证所得方程的△>0即可;
(2)①令抛物线的解析式中y=0,通过解方程即可求出A、B的坐标,进而可得到OA的长;易知C(0,-2a),由此可得到OC的长,在Rt△OAC中,根据勾股定理即可得到关于a的方程,可据此求出a的值,即可确定抛物线的解析式;
②根据平移的性质,可用t表示出直线l′的解析式以及A′、B′的坐标;由于抛物线在向右平移的过程中,开口大小没有变化,因此A′B′的长度和AB相等,由此可得到A′B′的长;若△A′B′P是以A'B'为直角边的等腰直角三角形,那么可有两种情况:
①∠PA'B'=90°,此时PA′=A′B′;②∠PB'A'=90°,此时PB′=A′B′;
根据PA′、PB′的表达式及A′B′的长,即可求出t的值.
点评:此题是二次函数的综合题,涉及到根的判别式、勾股定理、二次函数解析式的确定、等腰直角三角形的判定和性质等知识,需注意的是在等腰直角三角形的直角顶点不确定的情况下,要分类讨论,以免漏解.

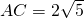 时,求抛物线的解析式;
时,求抛物线的解析式;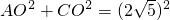 ,a2+(2a)2=20,
,a2+(2a)2=20, 或
或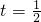
 或
或 (不合题意,舍去)
(不合题意,舍去) 或
或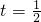 .
.

 名校课堂系列答案
名校课堂系列答案