

分析 (1)根据音乐的人数和所占的百分比即可求出总人数;用绘画的人数比上总人数即可求出选择“绘画”的学生人数占抽样人数的百分比;
(2)用总人数减去音乐、绘画和舞蹈的人数,求出体育的人数,再乘以360度即可得出体育所在扇形的圆心角的度数;
(3)用全校的总人数乘以选择“绘画”的学生所占的百分比即可得出答案.
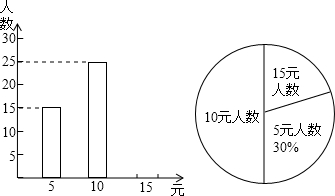
解答 解:(1)此次调查抽样的学生人数为$\frac{20}{20%}$=100(人);
其中选择“绘画”的学生人数占抽样人数的百分比为$\frac{40}{100}$=40%;
故答案为:100,40%;
(2)抽查的体育的人数是:100-20-40-10=30(人)
体育所在扇形的圆心角的度数是:360×$\frac{30}{100}$=108°;
补图如下:
故答案为:108;
(3)根据题意得:
2000×$\frac{40}{100}$=800(人),
答:估计全校选择“绘画”的学生大约有800人.
点评 本题考查的是条形统计图和扇形统计图的综合运用;读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键,是一道基础题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
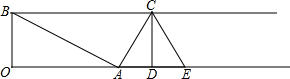 如图,射线BC∥射线OA,BO⊥OA,且OB=2,OA=4,过点A作AC⊥AB交射线BC于C,过点C作CD⊥射线OA交射线OA于D,A,E关于直线CD对称,将△CDE沿射线BC向左向右平移得到△C′D′E′.再将以A,B,C′,E′为顶点的四边形沿着C′D′剪开得到的两个图形拼成不重叠无缝隙的图形恰好是三角形,请写出所有符合上述条件的BC′的长6或1.
如图,射线BC∥射线OA,BO⊥OA,且OB=2,OA=4,过点A作AC⊥AB交射线BC于C,过点C作CD⊥射线OA交射线OA于D,A,E关于直线CD对称,将△CDE沿射线BC向左向右平移得到△C′D′E′.再将以A,B,C′,E′为顶点的四边形沿着C′D′剪开得到的两个图形拼成不重叠无缝隙的图形恰好是三角形,请写出所有符合上述条件的BC′的长6或1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
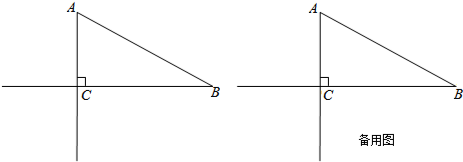
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
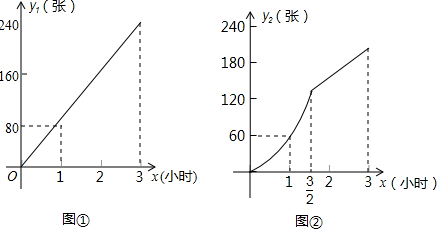
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.25≤x<1.35 | B. | 1.295≤x<1.305 | C. | 1.25<x<1.35 | D. | 1.295<x<1.305 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知抛物线y=x2-4x+3与x轴交于A,B两点,与y轴交于点C,顶点为E,把这条抛物线向上平移,使得抛物线的顶点落在x轴上,那么两条抛物线、对称轴和y轴围成的图形的面积S(图中阴影部分)为2.
如图,已知抛物线y=x2-4x+3与x轴交于A,B两点,与y轴交于点C,顶点为E,把这条抛物线向上平移,使得抛物线的顶点落在x轴上,那么两条抛物线、对称轴和y轴围成的图形的面积S(图中阴影部分)为2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com