
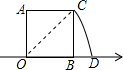
 如图,以数轴的单位长线段为边作一个正方形AOBC,以数轴的原点圆心,对角线OC为半径画弧,交数轴于点D,则点D表示的数是$\sqrt{2}$.
如图,以数轴的单位长线段为边作一个正方形AOBC,以数轴的原点圆心,对角线OC为半径画弧,交数轴于点D,则点D表示的数是$\sqrt{2}$.  开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m>$\frac{2}{3}$ | B. | m>$\frac{1}{2}$ | C. | m<$\frac{1}{2}$ | D. | m<$\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
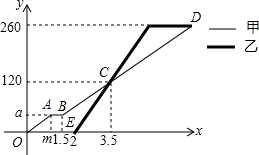 甲、乙两台机器各自加工相同数量的零件,工作时工作效率不变,甲机器先开始工作,中途停机检修了0.5小时.如图是甲、乙两台机器在整个工作过程中各自加工的零件个数y(个)与甲机器工作时间x(时)之间的函数图象.
甲、乙两台机器各自加工相同数量的零件,工作时工作效率不变,甲机器先开始工作,中途停机检修了0.5小时.如图是甲、乙两台机器在整个工作过程中各自加工的零件个数y(个)与甲机器工作时间x(时)之间的函数图象.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2016}$+$\sqrt{2016}$=$\sqrt{4032}$ | B. | $\sqrt{201{6}^{2}-(\frac{1}{2016})^{2}}=2016-\frac{1}{2016}$ | ||
| C. | $\sqrt{2016}×\sqrt{4032}$=2016$\sqrt{2}$ | D. | $\sqrt{2016}÷\sqrt{2}=1008$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | 3 | C. | $\frac{2\sqrt{2}}{3}$ | D. | $\frac{3\sqrt{2}}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com