
 ��ͼ��������y=-$\frac{1}{2}$x2+mx+2��x�ύ��A��B���㣬��y�ύ�ڵ�C�������ߵĶԳ���ֱ��x=$\frac{3}{2}$��x���ڵ�D��
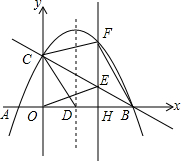
��ͼ��������y=-$\frac{1}{2}$x2+mx+2��x�ύ��A��B���㣬��y�ύ�ڵ�C�������ߵĶԳ���ֱ��x=$\frac{3}{2}$��x���ڵ�D������ ��1�����ݶԳ��ṫʽ���ɵ�M��ֵ��
��2�����ݵ��������εĶ��壬�ɵ�P�����ꣻ
��3������ƽ����y���ֱ���������ľ����ǽϴ�����������С�������꣬�ɵ�EF�ij������������ε������ʽ���ɵö��κ��������ݶ��κ��������ʣ��ɵ�n��ֵ������ƽ���ı��ε��ж����ɵô𰸣�
��� �⣺��1���߶Գ�����ֱ��x=$\frac{3}{2}$��
��-$\frac{m}{2����-\frac{1}{2}��}$=$\frac{3}{2}$��
��m=$\frac{3}{2}$��
��2���ɹ��ɶ�������
CD=$\frac{5}{2}$����CD=DP=$\frac{5}{2}$ʱ��P��$\frac{3}{2}$��$\frac{5}{2}$������$\frac{3}{2}$��-$\frac{5}{2}$����
��CD=CPʱ����P������Ϊ��$\frac{3}{2}$��b����
��$\sqrt{��\frac{3}{2}��^{2}+��b-2��^{2}}$=$\frac{5}{2}$��
���b=4��P��$\frac{3}{2}$��4����
����������P1��$\frac{3}{2}$��$\frac{5}{2}$����P2��$\frac{3}{2}$��-$\frac{5}{2}$����P3��$\frac{3}{2}$��4����
��3���ı���OCFE��ƽ���ı��Σ�
��������y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2��
��y=0��-$\frac{1}{2}$x2+$\frac{3}{2}$x+2=0�����x1=-1��x2=4��
��B��4��0����A��-1��0����
��x=0ʱ��y=2����C��0��2����
��BC�Ľ���ʽΪy=kx+b����B��4��0����C��0��2�����룬��
$\left\{\begin{array}{l}{4k+b=0}\\{b=2}\end{array}\right.$�����$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=2}\end{array}\right.$��
ֱ��BC����ʽΪy=-$\frac{1}{2}$x+2��
��F���������ϣ���F������Ϊ��n��-$\frac{1}{2}$n2+$\frac{3}{2}$n+2����
��E��BC�ϣ�E�������Ϊ��n��-$\frac{1}{2}$n+2����
EF=FH-EH=-$\frac{1}{2}$n2+2n��
��S�ı���CDBF=S��CDB+SCFB��
SCDB=$\frac{1}{2}$BD•CO=$\frac{1}{2}$����4-1.5����2=$\frac{5}{2}$��SCFB=$\frac{1}{2}$EF•OB•OB=$\frac{1}{2}$��4����-$\frac{1}{2}$n2+2n��=-n2+4n��
S�ı���CDBF=-n2+4n+$\frac{5}{2}$=-��n-2��2+$\frac{13}{2}$��
��n=2ʱ���ı���CDBF��������ʱEF=-$\frac{1}{2}$n2+2n=2��EH=-$\frac{1}{2}$n+2=1��OH=2��OE=$\sqrt{O{H}^{2}+E{H}^{2}}$=$\sqrt{5}$��
��OC=EF=2��OC��EF��
���ı���OCFE��ƽ���ı��Σ�
���� ���⿼���˶��κ����ۺ��⣬���õ��������εĶ���ó�CD=DP��CD=CP�ǽ���ؼ�����������ĺͲ�ó����κ����ǽ���ؼ�����������ƽ���ı��ε��ж���


 ����ѧ���ʱѧ����ϵ�д�
����ѧ���ʱѧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �Խ���� | B�� | �Խ������ | C�� | �Խ�����ƽ�� | D�� | �Ա���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
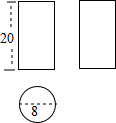 ��ͼ����������ͼȷ���ü������ȫ���Ϊ��ͼ�гߴ絥λ��cm����������
��ͼ����������ͼȷ���ü������ȫ���Ϊ��ͼ�гߴ絥λ��cm����������| A�� | 128��cm2 | B�� | 160��cm2 | C�� | 176��cm2 | D�� | 192��cm2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
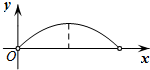 ��֪��MΪij���ͼ�α߽���һ���㣬����P�ӵ�M����������߽���ʱ���˶�һ�ܣ����P�߹���·��Ϊx���߶�MP�ij�Ϊy����ʾy��x�ĺ�����ϵ��ͼ�������ͼ��ʾ����÷��ͼ�ο����ǣ�������
��֪��MΪij���ͼ�α߽���һ���㣬����P�ӵ�M����������߽���ʱ���˶�һ�ܣ����P�߹���·��Ϊx���߶�MP�ij�Ϊy����ʾy��x�ĺ�����ϵ��ͼ�������ͼ��ʾ����÷��ͼ�ο����ǣ�������| A�� | 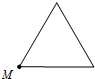 | B�� | 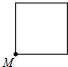 | C�� |  | D�� | 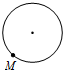 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
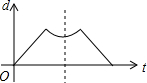 ��Բ������ֱ�������Ρ������κ͵��������α߽��ϵ�һ������ΪQ�����ĸ�ѡ���е�ͼ�Σ�������P�ӵ�Q����������߽��ϰ�˳ʱ�뷽�������˶�һ�ܺ��ֻص����Q�����P�˶���ʱ����t����P�͵�Q֮��ľ�����d����ͼ��d��t֮�亯����ϵ�Ĵ���ͼ�����ͼ�ο����ǣ�������
��Բ������ֱ�������Ρ������κ͵��������α߽��ϵ�һ������ΪQ�����ĸ�ѡ���е�ͼ�Σ�������P�ӵ�Q����������߽��ϰ�˳ʱ�뷽�������˶�һ�ܺ��ֻص����Q�����P�˶���ʱ����t����P�͵�Q֮��ľ�����d����ͼ��d��t֮�亯����ϵ�Ĵ���ͼ�����ͼ�ο����ǣ�������| A�� |  | B�� | 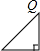 | C�� | 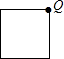 | D�� | 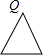 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ֱ��y=$\frac{1}{2}$x-2��x�ύ�ڵ�A����y�ύ�ڵ�C��������y=ax2+bx-2����A��B��C����B����Ϊ��-1��0����
��ͼ��ֱ��y=$\frac{1}{2}$x-2��x�ύ�ڵ�A����y�ύ�ڵ�C��������y=ax2+bx-2����A��B��C����B����Ϊ��-1��0�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
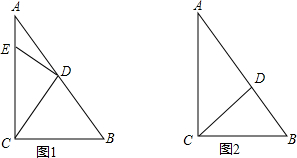
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | S32��S22��S12 | B�� | S12=S22��S32 | C�� | S12=S22��S32 | D�� | S12=S22=S32 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{8}$ | B�� | $\frac{1}{9}$ | C�� | $\frac{1}{12}$ | D�� | $\frac{1}{15}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com