练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    若|a|=b+1，b=2，且ab＜0，求4a-|b-2（b+a）+2a|的值．
    考点：整式的加减—化简求值,绝对值
    专题：计算题
    分析：利用绝对值的代数意义及a与b异号，求出a的值，原式绝对值里边去括号合并后，将a与b的值代入计算即可求出值．
    解答：解∵|a|=b+1，b=2，
    ∴|a|=3，即a=±3；
    ∵ab＜0，∴a=-3，
    则4a-|b-2（b+a）+2a|=4a-|b-2b-2a+2a|=4a-|b|=4×（-3）-|2|=-14．
    点评：此题考查了整式的加减-化简求值，熟练掌握运算法则是解本题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

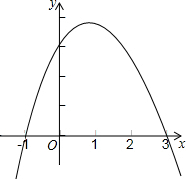    二次函数y=ax2+bx+c（a、b、c是常数a≠0）的大致图象如图所示，抛物线交x轴于点（-1，0），（3，0）．若函数y的值随着x的增大而增大，则x的取值范围是（　　）
    A、x≤1B、x≤-1
    C、x≥1D、x≥3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    下列说法中正确的是（　　）
    A、1是单项式
    B、单项式m的系数为0，次数为0
    C、单项式2a2b的系数是2，次数是2
    D、xy-x+y-4的项是xy，x，y，4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

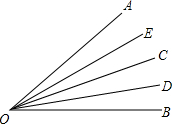    已知：如图，∠AOB=40°，OC平分∠AOB，OD、OE分别平分∠BOC和∠AOC．
    求：
    （1）∠DOE的度数．
    （2）当OC在∠AOB内绕O点旋转时，OD、OE仍是∠BOC和∠AOC的平分线．问此时∠DOE的大小是否和（1）中的答案相同？说明理由，通过此过程你能总结出怎样的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    定义：在平面直角坐标系xOy中，对于任意两点P1（x1，y1）与P2（x2，y2）的“非常距离”，给出如下定义：若|x1-x2|≥|y1-y2|，则点P1与点P2的“非常距离”为|x1-x2|；若|x1-x2|＜|y1-y2|，则点P1与点P2的“非常距离”为|y1-y2|．
    （1）已知点A（-
    1
    2
    ，0），B为y轴上的一个动点，若点A与点B的“非常距离”为2，写出 一个满足条件的点B的坐标
     
    ；
    （2）已知C是直线y=
    		3
    x+3上的一个动点，点D的坐标是（0，1），当CD与直线y=
    		3
    x+3垂直时，求C与D的“非常距离”．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图用一张边长为16cm的正方形纸片，在其四个角上减掉四个边长相同的小正方形可做成无盖的长方体盒子．若设减掉的小正方形的边长为xcm，做成的无盖长方体盒子的容积为Vcm2．
    （1）要使做成的长方体盒子底面周长为48cm，那么减掉的正方形边长为
     
    cm；
    （2）用含x的式子表示V=
     
    ；
    （3）填表：
     x（cm）  1 2  3  4  5 
     V（cm2）
     
     
     
     
     
     
     
    观察表格中的结果，你能得到那些信息？（写出两条）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （神奇的数学游戏）根据下面的游戏向导来试着玩这个游戏．写出一个你喜欢的数，把这个数加上3，把结果乘以5，再减去15，再除以5，结果你会重新得到原来的数．
    （1）假设一开始写出的数为n，根据这个游戏的每一步，列出最后的表达式．
    （2）将（1）中得到的表达式进行化简．用你的结果来证实：为什么游戏对任意数都成立．
    （3）自己编写一个数学游戏，并写出步骤（试着使你编出的游戏让人感到惊奇，且最好不是显而易见的）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，已知AB是⊙O的直径，点C，D在⊙O上，且AB=6，BC=3．
    （1）求∠ADC的度数；
    （2）如果OE⊥AC，垂足为E，求OE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    4x2-xy-(
    4
    3
    y2+2x2)+2(3xy-
    1
    3
    y2)    ，其中x=5，y=
    1
    2
    ．

    查看答案和解析>>

    同步练习册答案