
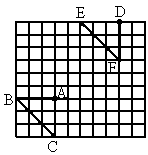
如图,小方格表示边长为1的正方形.把△BAC向___________移动__________单位,再向_________移动__________个单位.△BAC和△EDF重合.(只要写出一种方法).
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案科目:初中数学 来源: 题型:阅读理解

查看答案和解析>>
科目:初中数学 来源: 题型:044
(1)在区域MNCD内,请你针对图①,图②,图③,图④中列车位于不同位置的情形分别画出相应的盲区,并在盲区内涂上阴影.
(2)只考虑在区域ABCD内形成的盲区.设在这个区域内的盲区面积是y(平方单位).
①如图⑤,当5≤t≤10时,请你求出用t表示y的函数关系式;
②如图⑥,当10≤t≤15时,请你求出用t表示y的函数关系式;
③如图⑦,当15≤t≤20时,请你求出用t表示y的函数关系式;
④根据①棦壑械玫降慕崧郏?肽慵虻ジ爬▂随t的变化而变化的情况.
(3)根据上述研究过程,请你按不同的时段,就列车行驶过程中在区域MNCD内所形成盲区的面积大小的变化情况提出一个综合的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:022
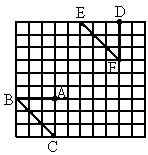
如图,小方格表示边长为1的正方形.把△BAC向___________移动__________单位,再向_________移动__________个单位.△BAC和△EDF重合.(只要写出一种方法).
查看答案和解析>>
科目:初中数学 来源:北京模拟题 题型:解答题
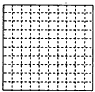
人们经常利用图形的规律来计算一些数的和.如在每个小方格的边长均为1的网格图(1)中,从左下角开始,相邻的黑折线围成的面积分别是1,3,5,7,9,11,13,15,17,…,它们有下面的规律:
1+3=22;
1+3+5=32;
1+3+5+7=42;
1+3+5+7+9=52;
......

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com