
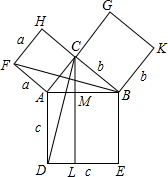
 △ABC是以∠ACB为直角的直角三角形,以AB、BC、AC为边作正方形ABED、BCGK、ACHF,过点C作CL⊥DE交AB于点M,交DE于点L,连接CD、BF.求证:a2+b2=c2.
△ABC是以∠ACB为直角的直角三角形,以AB、BC、AC为边作正方形ABED、BCGK、ACHF,过点C作CL⊥DE交AB于点M,交DE于点L,连接CD、BF.求证:a2+b2=c2. 分析 先判断出点H,C,B在同一条直线上,再求出三角形FAB的面积,从而判断出△FAB≌△CAD即可得出三角形CAD的面积是矩形ADLM的面积的一半,即矩形的面积等于a2,同理得出矩形MLEB的面积等于b2,最后用两个矩形的面积之和等于边长为c的正方形的面积,化简即可.
解答 证明:做三个边长分别以a,b,c的正方形,把它们拼成如图所示的形状,
连接BF,CD,过点C作CL⊥DE,交AB于点M,交DE于点L,
∵四边形ACHF是正方形,
∴∠ACH=90°,
∵∠ACB=90°,
∴∠ACH+∠ACB=180°,
∴H,C,B在同一条直线上,
∴S△FAB=S梯形ABHF-S△BHF=$\frac{1}{2}$a[a+(a+b)]-$\frac{1}{2}$a(a+b)=$\frac{1}{2}$a2,
∵四边形ABED,ACHF是正方形,
∴AF=AC,AB=AD,∠CAF=∠BAD=90°,
∴∠FAB=∠CAD,
在△FAB和△CAD中$\left\{\begin{array}{l}{AF=AC}\\{∠FAB=∠CAD}\\{AB=AD}\end{array}\right.$,
∴△FAB≌△CAD,
∴S△CAD=S△FAB=$\frac{1}{2}$a2,
同理:S△CAD=$\frac{1}{2}$S矩形ADLM,
∴S矩形ADLM=a2,
同理:S矩形MLEB=b2,
∵S矩形ADLM+S矩形MLEB=S正方形ADEB,
∴a2+b2=c2.
点评 此题是正方形的性质,主要考查了正方形的性质,面积公式,梯形的面积公式,解本题的关键是得出矩形ADLM面积等于a2.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 如图,某仓储中心有一斜坡AB,其坡度为i=1:2,顶部A处的高AC为4m,B、C在同一水平地面上.
如图,某仓储中心有一斜坡AB,其坡度为i=1:2,顶部A处的高AC为4m,B、C在同一水平地面上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在等边△ABC中,P是BC下方一动点,且∠BPC=120°,PB、PC是关于x的方程(a-1)x2-9(a-1)x+b=c的两实数根,求PA的长.
如图,在等边△ABC中,P是BC下方一动点,且∠BPC=120°,PB、PC是关于x的方程(a-1)x2-9(a-1)x+b=c的两实数根,求PA的长.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
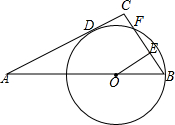 如图,Rt△ABC,∠C=90°,BC=3,点O在AB上,OB=2,以OB长为半径的⊙O与AC相切于点D,交BC于点F,OE⊥BC于点E,则弦BF的长为2.
如图,Rt△ABC,∠C=90°,BC=3,点O在AB上,OB=2,以OB长为半径的⊙O与AC相切于点D,交BC于点F,OE⊥BC于点E,则弦BF的长为2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com