
(12分)如图,点A(m,m+1),B(m+3,m-1)都在反比例函数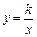 的图象上.
的图象上.  (1)求m,k的值;
(1)求m,k的值;
(2)如果M为x轴上一点,N为y轴上一点,
以点A,B,M,N为顶点的四边形是平行四边形,
试求直线MN的函数表达式.
解:(1)由题意可知,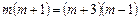 .
.
解,得 m=3.  ………………………………3分
………………………………3分
∴ A(3,4),B(6,2); 
∴ k=4×3=12. ……………………………4分
(2)存在两种情况,如图:
①当M点在x轴的正半轴上, N点在y轴的正半轴
N点在y轴的正半轴
上时,设M1点坐标为(x1,0),N1点坐标为(0,y1).
∵ 四边形AN1M1B为平行四边形,
∴ 线段N1M1可看作由线段AB向左平移3个单位,
再向下平移 2个单位得到的(也可看作向下平移2个单位,再向左平移3个单位得到的).
2个单位得到的(也可看作向下平移2个单位,再向左平移3个单位得到的).
由(1)知A点坐标为(3,4),B点坐标为(6,2),
∴ N1点坐标为(0,4-2),即N1(0,2);
M1点坐标为(6-3,0),即M1 (3,0)
(3,0) .
.
设直线M1N1的函数表达式为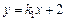 ,把x=3,y=0代入,解得
,把x=3,y=0代入,解得 .
.
∴ 直线M1N1的函数表达式为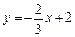 .
.
②当M点在x轴的负半轴上,N点在y轴的负半轴上时,设M2点坐标为(x2,0),N2点坐标为(0,y2).
∵ AB∥N1M1,AB∥M2N2,AB=N1M1,AB=M2N2,
∴ N1M1∥M2N2,N1M1=M2N2.
∴ 线段M2N2与 线段N1M1关于原点O成中心对称.
线段N1M1关于原点O成中心对称.
∴ M2点坐标为(-3,0),N2点坐标为(0,-2).
设直线M2N2的函数表达式为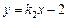 ,把x=-3,y=0代入,解得
,把x=-3,y=0代入,解得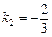 ,
,
∴ 直线M2N2的函数表达式为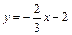 .
. 
所以,直线MN的函数表达式为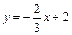 或
或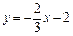 .
.
解析


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
(本题12分)如图,点O是等边△ABC内一点,D是△ABC外的一点, ∠AOB= 110°,
∠BOC= ![]() ,△BOC ≌△ADC,∠OCD=60°,连接OD。
,△BOC ≌△ADC,∠OCD=60°,连接OD。
(1)求证:△OCD是等边三角形;
(2)当![]() =150°时,试判断△AOD 的形状,并说明理由;
=150°时,试判断△AOD 的形状,并说明理由;
(3)探究:当![]() 为多少度时,△AOD是等腰三角形。
为多少度时,△AOD是等腰三角形。

查看答案和解析>>
科目:初中数学 来源: 题型:
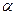 ,△BOC ≌△ADC,∠OCD=60°,连接OD。
,△BOC ≌△ADC,∠OCD=60°,连接OD。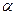 =150°时,试判断△AOD 的形状,并说明理由;
=150°时,试判断△AOD 的形状,并说明理由;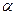 为多少度时,△AOD是等腰三角形。
为多少度时,△AOD是等腰三角形。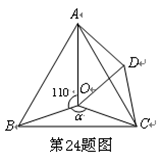
查看答案和解析>>
科目:初中数学 来源:2011-2012学年浙江省杭州市萧山区临浦片八年级上学期期中质量检测数学卷 题型:解答题
(本题12分)如图,点O是等边△ABC内一点,D是△ABC外的一点, ∠AOB= 110°,
∠BOC= 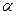 ,△BOC ≌△ADC,∠OCD=60°,连接OD。
,△BOC ≌△ADC,∠OCD=60°,连接OD。
(1)求证:△OCD是等边三角形;
(2)当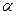 =150°时,试判断△AOD 的形状,并说明理由;
=150°时,试判断△AOD 的形状,并说明理由;
(3)探究:当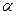 为多少度时,△AOD是等腰三角形。
为多少度时,△AOD是等腰三角形。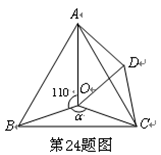
查看答案和解析>>
科目:初中数学 来源:2013届浙江省杭州市萧山区临浦片八年级上学期期中质量检测数学卷 题型:解答题
(本题12分)如图,点O是等边△ABC内一点,D是△ABC外的一点, ∠AOB= 110°,
∠BOC= 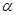 ,△BOC ≌△ADC,∠OCD=60°,连接OD。
,△BOC ≌△ADC,∠OCD=60°,连接OD。
(1)求证:△OCD是等边三角形;
(2)当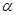 =150°时,试判断△AOD 的形状,并说明理由;
=150°时,试判断△AOD 的形状,并说明理由;
(3)探究:当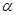 为多少度时,△AOD是等腰三角形。
为多少度时,△AOD是等腰三角形。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com