
 画一个以a为边的正六边形(要求尺规作图,并要求写作法,保留作图痕迹)
画一个以a为边的正六边形(要求尺规作图,并要求写作法,保留作图痕迹)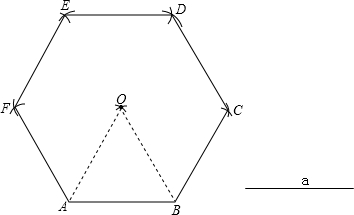 解:作法:(1)作线段AB=a,分别以A、B为圆心,以a长为半径画弧相交于点O;
解:作法:(1)作线段AB=a,分别以A、B为圆心,以a长为半径画弧相交于点O;

 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
 两只大小不同的含45°角的三角板ABC和DBE如图摆放,直角顶点重合,连接AE,CD,F,M,N,G分别为线段AC,CD,ED,AE的中点.
两只大小不同的含45°角的三角板ABC和DBE如图摆放,直角顶点重合,连接AE,CD,F,M,N,G分别为线段AC,CD,ED,AE的中点.查看答案和解析>>
科目:初中数学 来源: 题型:
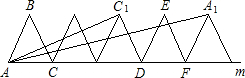 如图,已知边长为2的正三角形ABC沿直线m滚动,当△ABC滚动一周时,到△DEF位置.设△ABC滚动240°时,点C的位置为C1,△ABC滚动480°时,点A的位置为点A1.根据三角函数正切的两角和公式tan(α+β)=
如图,已知边长为2的正三角形ABC沿直线m滚动,当△ABC滚动一周时,到△DEF位置.设△ABC滚动240°时,点C的位置为C1,△ABC滚动480°时,点A的位置为点A1.根据三角函数正切的两角和公式tan(α+β)=| tanα+tanβ |
| 1-tanα•tanβ |
查看答案和解析>>
科目:初中数学 来源: 题型:
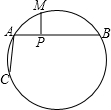 已知M是弧CAB的中点,MP垂直弦AB于P,若弦AC的长度为x,线段AP的长度是x+1,那么线段PB的长度是( )
已知M是弧CAB的中点,MP垂直弦AB于P,若弦AC的长度为x,线段AP的长度是x+1,那么线段PB的长度是( )| A、2x+1 | B、2x+2 |
| C、2x+3 | D、3x+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com