
【题目】在平面直角坐标系xOy中,函数y=![]() (x>0)的图象与直线y=
(x>0)的图象与直线y=![]() x+1交于点A(2,m).
x+1交于点A(2,m).
(1)求k、m的值;
(2)已知点P(n,0),过点P作平行于 y 轴的直线,交直线y=![]() x+1于点B,交函数y=
x+1于点B,交函数y=![]() (x>0)的图象于点C.若y=
(x>0)的图象于点C.若y=![]() (x>0)的图象在点A、C之间的部分与线段AB、BC所围成的区域内(不包括边界),记作图形G.横、纵坐标都是整数的点叫做整点.
(x>0)的图象在点A、C之间的部分与线段AB、BC所围成的区域内(不包括边界),记作图形G.横、纵坐标都是整数的点叫做整点.
①当n=4时,直接写出图形G的整点坐标;
②若图形G 恰有2 个整点,直接写出n的取值范围.
【答案】(1)k=4,m=2;(2)①(3,2),②0<n<1或4<n<5.
【解析】
(1)将A点代入直线解析式可求m,再代入y=![]() ,可求k.
,可求k.
(2)①根据题意先求B,C两点,可得图形G的整点的横坐标的范围2<x<4,且x为整数,所以x取3.再代入可求整点的纵坐标的范围,即求出整点坐标.
②根据图象可以直接判断2≤n<3.
解:(1)∵点A(2,m)在y=![]() x+1上,
x+1上,
∴m=![]() ×2+1=2.
×2+1=2.
∴A(2,2).
∵点A(2,2)在函数y=![]() 的图象上,
的图象上,
∴k=4.
故答案为:k=4,m=2.
(2)①当n=4时,B、C两点的坐标为B(4,3)、C(4,1).
∵整点在图形G的内部,
∴2<x<4且x为整数
∴x=3
∴将x=3代入y=![]() x+1得y=2.5,
x+1得y=2.5,
将x=3代入y=![]() 得y=
得y=![]() ,
,
∴![]() <y<2.5,
<y<2.5,
∵y为整数,
∴y=2,
∴图形G的整点坐标为(3,2).
②当x=3时,![]() <y<2.5,此时的整点有(3,2)共1个;
<y<2.5,此时的整点有(3,2)共1个;
当x=4时,1<y<3,此时的整点有(4,2)共1个;
当x=5时,![]() <y<3.5,此时的整点有(5,1),(5,2),(5,3)共3个;
<y<3.5,此时的整点有(5,1),(5,2),(5,3)共3个;
∵图形G 恰有2 个整点,
∴4<n<5,
当x=1时,1.5<y<4,此时的整点有(1,2),(1,3)共2个;
∵图形G 恰有2 个整点,
∴0<n<1,
综上所述,n的取值范围为:0<n<1或4<n<5.


科目:初中数学 来源: 题型:
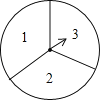
【题目】如图,转盘被平均分成三块扇形,转动转盘,转动过程中,指针保持不动,转盘停止后,如果指针恰好指在分割线上,则重转一次,直到指针指向一个数字所在的区域为止.
(1)转动转盘两次,用画树状图或列表的方法求两次指针所指区域数字不同的概率;
(2)在第(1)题中,两次转到的区域的数字作为两条线段的长度,如果第三条线段的长度为5,求这三条线段能构成三角形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下列10×10的网格中,横、纵坐标均为整数的点叫做格点,例如A(3,0),B(4,3)都是格点.将△AOB绕点O顺时针旋转90°得到△COD(点A,B的对应点分别为点C,D).
(1)作出△COD;
(2)下面仅用无刻度的直尺画△AOD的内心I,操作如下:
第一步:在x轴上找一格点E,连接DE,使OE=OD;
第二步:在DE上找一点F,连接OF,使OF平分∠AOD;
第三步:找格点G,得到正方形OAGC,连接AC,则AC与OF的交点I是△OAD的内心.
请你按步骤完成作图,并直接写出E,F,I三点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】吉祥超市准备购进甲、乙两种绿色袋装食品共800袋.甲、乙两种绿色袋装食品的进价和售价如表.已知:用2000元购进甲种袋装食品的数量与用1600元购进乙种袋装食品的数量相同.
甲 | 乙 | |
进价(元/袋) | m | m﹣2 |
售价(元/袋) | 20 | 13 |
(1)求m的值;
(2)假如购进的甲、乙两种绿色袋装食品全部卖出,所获总利润不少于5200元,且不超过5280元,问该超市有几种进货方案?(利润=售价﹣进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
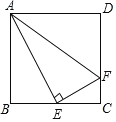
【题目】如图,在正方形ABCD中,E是BC的中点,F是CD上一点,AE⊥EF.有下列结论:①∠BAE=30°;②射线FE是∠AFC的角平分线;③AE2=ADAF;④AF=AB+CF.其中正确结论为是______.(填写所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
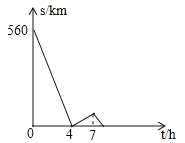
【题目】一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后分别按原速同时驶往甲地,两车之间的距离S(km)与慢车行驶时间t(h)之间的函数图象如图所示,下列说法:
①甲、乙两地之间的距离为560km;
②快车速度是慢车速度的1.5倍;
③快车到达甲地时,慢车距离甲地60km;
④相遇时,快车距甲地320km;
其中正确的个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.

(1)求证:△AEC≌△ADB;(2)若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
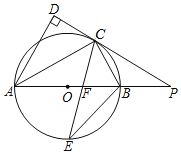
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,AC平分∠DAB,直线DC与AB的延长线相交于点P,AD与PC延长线垂直,垂足为点D,CE平分∠ACB,交AB于点F,交⊙O于点E.
(1)求证:PC与⊙O相切;
(2)求证:PC=PF;
(3)若AC=8,tan∠ABC=![]() ,求线段BE的长.
,求线段BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为直径作圆
为直径作圆![]() ,分别交
,分别交![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() 交线段
交线段![]() 于点
于点![]() .
.
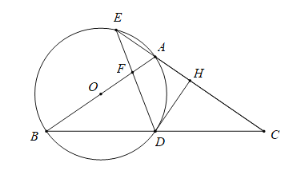
(1)求证:![]() 是圆
是圆![]() 的切线;
的切线;
(2)若![]() 为
为![]() 的中点,求
的中点,求![]() 的值;
的值;
(3)若![]() ,求圆
,求圆![]() 的半径.
的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com