练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在Rt△ABC中，∠ACB=90°，AC=6，BC=12，点D在边BC上，点E在线段AD上，EF⊥AC于点F，EG⊥EF交AB于点G，若EF=EG，则CD的长为（ ）

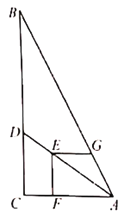
    A.3.6B.4C.4.8D.5

    【答案】B

    【解析】

    过点D作DH⊥BC交AB于点H，根据△AFE∽△ACD和△AEG∽△ADH可得DC=DH，再由△BDH∽△BCA，根据相似三角形的性质列出方程即可求出CD.

    解：过点D作DH⊥BC交AB于点H，

    ∵EF⊥AC，∴EF∥BC，

    ∴△AFE∽△ACD，∴，

    ∵DH⊥BC，EG⊥EF，∴DH∥EG，

    ∴△AEG∽△ADH，∴，

    ∴

    ∵EF=EG，

    ∴DC=DH，

    设DH=DC=x，则BD=12-x，

    又∵△BDH∽△BCA，

    ∴，即，

    解得：x=4，即CD=4，

    故选B.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，AD∥BC，∠EAD＝∠C．

    （1）试判断AE与CD的位置关系，并说明理由；

    （2）若∠FEC＝∠BAE，∠EFC＝50°，求∠B的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，O是边长为6的等边△ABC三边中垂线的交点，将△ABC绕点O逆时针方向旋转180°，得到△A1B1C1，则图中阴影部分的面积为_____．

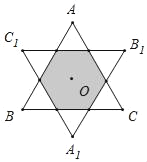
    查看答案和解析>>

    科目：初中数学 来源： 题型：

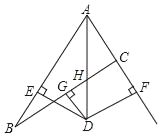
    【题目】如图，在△ABC中，AD平分∠BAC，DG⊥BC且平分BC于点G，DE⊥AB于点E，DF⊥AC交AC的延长线于点F．

    （1）求证：AE＝AF；

    （2）求证：BE＝CF；

    （3）如果AB＝12，AC＝8，求AE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知抛物线过点A（2，0），B（﹣1，0），与y轴交于点C，且OC=2，求这条抛物线的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

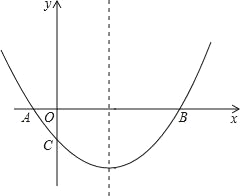
    【题目】如图，抛物线经过A（﹣1，0），B（5，0），C（0， ）三点．

    （1）求抛物线的解析式；

    （2）在抛物线的对称轴上有一点P，使PA+PC的值最小，求点P的坐标；

    （3）点M为x轴上一动点，在抛物线上是否存在一点N，使以A，C，M，N四点构成的四边形为平行四边形？若存在，求点N的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在中， ，点分别是的中点， 是延长线上的一点，且．

    （1）求证： ；

    （2）求证： ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某景区的门票销售分两类：一类为散客门票，价格为元/张；另一类为团体门票（一次性购买门票张以上），每张门票价格在散客门票价格的基础上打折，某班部分同学要去该景点旅游，设参加旅游人，购买门票需要元

    （1）如果每人分别买票，求与之间的函数关系式：

    （2）如果购买团体票，求与之间的函数关系式，并写出自变量的取值范围；

    （3）请根据人数变化设计一种比较省钱的购票方式.

    查看答案和解析>>

    同步练习册答案