
【题目】每年的6月5日为世界环保日,为了提倡低碳环保,某公司决定购买10台节省能源的新设备,现有甲乙两种型号的设备可供选购.经调查:购买3台甲型设备比购买2台乙型设备多花14万元,购买2台甲型设备比购买3台乙型设备少花4万元.
(1)直接写出甲乙两种型号设备每台的价格分别为多少万元;
(2)该公司经预算决定购买节省能源的新设备的资金不超过90万元,你认为该公司有几种购买方案?
(3)在(2)的条件下,若该公司使用新设备进行生产,已知甲型设备每台的产量为240吨/月,乙型设备每台的产量为180吨/月,每月要求总产量不低于2040吨,请你为该公司设计一种最省钱的购买方案.
【答案】(1)甲型号每台10万元,乙型号每台8万元;(2)有6种购买方案;(3)最省钱的购买方案为:选购甲型设备4台,乙型设备6台.
【解析】
(1)设甲型设备每台的价格为x万元,乙型设备每台的价格为y万元,根据“购买3台甲型设备比购买2台乙型设备多花14万元,购买2台甲型设备比购买3台乙型设备少花4万元”,即可得出关于x、y的二元一次方程组,解之即可得出结论;
(2)设购买甲型设备m台,则购买乙型设备(10-m)台,由于购买节省能源的新设备的资金不超过90万元,即可得出关于m的一元一次不等式组,解之即可得出各购买方案;
(3)由每月要求总产量不低于2040吨,可得出关于m的一元一次不等式,解之结合(2)的结论即可找出m的值,再利用总价=单价×数量求出两种购买方案所需费用,比较后即可得出结论.
(1)设甲型号每台![]() 万元,乙型号每台
万元,乙型号每台![]() 万元,则
万元,则
![]() ,
,
解得![]() ;
;
![]() 甲型号每台
甲型号每台![]() 万元,乙型号每台
万元,乙型号每台![]() 万元
万元
(2)设购买甲型![]() 台,乙型
台,乙型![]() 台,根据题意得,
台,根据题意得,
![]() ,
,
解得,![]() ,
,
∵![]() 取非负整数 ,
取非负整数 ,
![]() ,
,
∴有6种购买方案;
(3)根据题意,得
![]() ,
,
解得,![]() ,
,
∴当![]() 时,购买资金为10×4+8×6=88(万元),
时,购买资金为10×4+8×6=88(万元),
当![]() 时,购买资金为10×5+8×5=90(万元),
时,购买资金为10×5+8×5=90(万元),
则最省钱的购买方案为:选购甲型设备4台,乙型设备6台.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的两个外角∠CBE,∠CDF的平分线交于点G,若∠A=52°,∠DGB=28°,则∠DCB的度数是( )
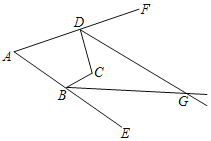
A. 152°B. 128°C. 108°D. 80°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一块材料的形状是锐角三角形ABC,边BC=120mm,高AD=80mm,把它加工成正方形零件如图1,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
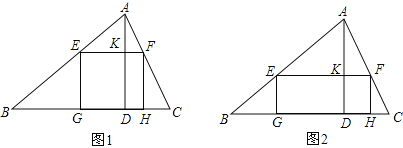
(1)求证:△AEF∽△ABC;
(2)求这个正方形零件的边长;
(3)如果把它加工成矩形零件如图2,问这个矩形的最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,与直线
,与直线![]() 相交于点
相交于点![]() .
.

(1)求点![]() 的坐标;
的坐标;
(2)请判断![]() 的形状并说明理由;
的形状并说明理由;
(3)动点![]() 从原点
从原点![]() 出发,以每秒
出发,以每秒![]() 个单位的速度沿着
个单位的速度沿着![]() 的路线向点
的路线向点![]() 匀速运动(
匀速运动(![]() 不与点
不与点![]() 、
、![]() 重合),过点
重合),过点![]() 分别作
分别作![]() 轴于
轴于![]() ,
,![]() 轴于
轴于![]() ,设运动
,设运动![]() 秒时,矩形
秒时,矩形![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
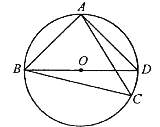
【题目】如图,![]() 为
为![]() 的外接圆上的一动点(点
的外接圆上的一动点(点![]() 不在
不在![]() 上,且不与点
上,且不与点![]() 、
、![]() 重合),
重合),![]() .
.
(1)求证:![]() 是该外接圆的直径;
是该外接圆的直径;
(2)连接![]() ,求证:涯
,求证:涯![]() ;
;
(3)若![]() 关于直线
关于直线![]() 的对称图形为
的对称图形为![]() ,连接
,连接![]() ,试探究
,试探究![]() 、
、![]() 、
、![]() 三者之间满足的等量关系,并证明你的结论.
三者之间满足的等量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】养成良好的早锻炼习惯,对学生的学习和生活都非常有益,某中学为了了解七年级学生的早锻炼情况,校政教处在七年级随机抽取了部分学生,并对这些学生通常情况下一天的早锻炼时间![]() (分钟)进行了调查.现把调查结果分成
(分钟)进行了调查.现把调查结果分成![]() 四组,如下表所示,同时,将调查结果绘制成下面两幅不完整的统计图.
四组,如下表所示,同时,将调查结果绘制成下面两幅不完整的统计图.

请根据以上的信息,解答下列问题:
(1)扇形统计图![]() 所在的圆心角的度数为 ;
所在的圆心角的度数为 ;
(2)补全频数分布直方图;
(3)已知该校七年级共有1000名学生,请你估计这个年级学生中约有多少人一天早锻炼的时间不少于20分钟.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,我国煤矿安全事故频频发生,其中危害最大的是瓦斯,其主要成分是CO.在一次矿难事件的调查中发现:从零时起,井内空气中CO的浓度达到4 mg/L,此后浓度呈直线型增加,在第7小时达到最高值46 mg/L,发生爆炸;爆炸后,空气中的CO浓度成反比例下降,如图,根据题中相关信息回答下列问题:
(1)求爆炸前后空气中CO浓度y与时间x的函数关系式,并写出相应的自变量取值范围;
(2)当空气中的CO浓度达到34 mg/L时,井下3 km的矿工接到自动报警信号,这时他们至少要以多少km/h的速度撤离才能在爆炸前逃生?
(3)矿工只有在空气中的CO浓度降到4 mg/L及以下时,才能回到矿井开展生产自救,求矿工至少在爆炸后多少小时才能下井?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC是边长为4的等边三角形,点O在边AB上,⊙O过点B且分别与边AB,BC相交于点D,E,EF⊥AC,垂足为F.
(1)求证:直线EF是⊙O的切线;
(2)当直线DF与⊙O相切时,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CD⊥AB,垂足为D,E是AC边上一点,EH⊥AB,垂足为H,∠1=∠2.
(1)试说明DF∥AC;
(2)若∠A=38°,∠BCD=45°,求∠3的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com