练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    19．如图，直角△ABC中，∠A为直角，AB=6，AC=8．点P，Q，R分别在AB，BC，CA边上同时开始作匀速运动，2秒后三个点同时停止运动，点P由点A出发以每秒3个单位的速度向点B运动，点Q由点B出发以每秒5个单位的速度向点C运动，点R由点C出发以每秒4个单位的速度向点A运动，在运动过程中：
    （1）求证：△APR，△BPQ，△CQR的面积相等；
    （2）求△PQR面积的最小值；
    （3）用t（秒）（0≤t≤2）表示运动时间，是否存在t，使∠PQR=90°？若存在，请直接写出t的值；若不存在，请说明理由．

    分析 （1）先利用锐角三角函数表示出QE=4t，QD=3（2-t），再由运动得出AP=3t，CR=4t，BP=3（2-t），AR=4（2-t），最后用三角形的面积公式即可得出结论；
    （2）借助（1）得出的结论，利用面积差得出S△PQR=18（t-1）2+6，即可得出结论；
    （3）先判断出∠DQR=∠EQP，用此两角的正切值建立方程求解即可．

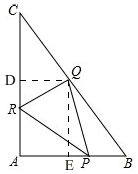    解答 解：（1）如图，在Rt△ABC中，AB=6，AC=8，根据勾股定理得，BC=10，sin∠B=$\frac{AC}{AB}$=$\frac{8}{10}$=$\frac{4}{5}$，sin∠C=$\frac{3}{4}$，
    过点Q作QE⊥AB于E，
    在Rt△BQE中，BQ=5t，
    ∴sin∠B=$\frac{QE}{BQ}$=$\frac{4}{5}$，
    ∴QE=4t，
    过点Q作QD⊥AC于D，
    在Rt△CDQ中，CQ=BC-BQ=10-5t，
    ∴QD=CQ•sin∠C=$\frac{3}{5}$（10-5t）=3（2-t），
    由运动知，AP=3t，CR=4t，
    ∴BP=AB-AP=6-3t=3（2-t），AR=AC-CR=8-4t=4（2-t），
    ∴S△APR=$\frac{1}{2}$AP•AR=$\frac{1}{2}$×3t×4（2-t）=6t（2-t），
    S△BPQ=$\frac{1}{2}$BP•QE=$\frac{1}{2}$×3（2-t）×4t=6t（2-t），
    S△CQR=$\frac{1}{2}$CR•QD=$\frac{1}{2}$×4t×3（2-t）=6t（2-t），
    ∴S△APR=S△BPQ=S△CQR，
    ∴△APR，△BPQ，△CQR的面积相等；

    （2）由（1）知，S△APR=S△BPQ=S△CQR=6t（2-t），
    ∵AB=6，AC=8，
    ∴S△PQR=S△ABC-（S△APR+S△BPQ+S△CQR）
    =$\frac{1}{2}$×6×8-3×6t（2-t）=24-18（2t-t2）=18（t-1）2+6，
    ∵0≤t≤2，
    ∴当t=1时，S△PQR最小=6；

    （3）存在，由点P，Q，R的运动速度知，运动1秒时，点P，Q，R分别在AB，BC，AC的中点，此时，四边形APQR是矩形，即：t=1秒时，∠PQR=90°，

    由（1）知，QE=4t，QD=3（2-t），AP=3t，CR=4t，AR=4（2-t），
    ∴BP=AB-AP=6-3t=3（2-t），AR=AC-CR=8-4t=4（2-t），
    过点Q作QD⊥AC于D，作QE⊥AB于E，∵∠A=90°，
    ∴四边形APQD是矩形，
    ∴AE=DQ=3（2-t），AD=QE=4t，
    ∴DR=|AD-AR|=|4t-4（2-t）|=4|2t-2|，PE=|AP-AE|=|3t-3（2-t）|=3|2t-2|
    ∵∠DQE=90°，∠PQR=90°，
    ∴∠DQR=∠EQP，
    ∴tan∠DQR=tan∠EQP，
    在Rt△DQR中，tan∠DQR=$\frac{DR}{DQ}$=$\frac{4|2t-2|}{3（2-t）}$，
    在Rt△EQP中，tan∠EQP=$\frac{PE}{QE}$=$\frac{3|2t-2|}{4t}$，
    ∴$\frac{4|2t-2|}{3（2-t）}=\frac{3|2t-2|}{4t}$，
    ∴16t=9（2-t），
    ∴t=$\frac{18}{25}$．
    即：t=1或$\frac{18}{25}$秒时，∠PQR=90°．

    点评 此题是三角形综合题，主要考查了勾股定理，锐角三角函数，矩形的判定和性质，三角形的面积公式，解（1）的关键是求出QD，QE，解（2）的关键是建立函数关系式，解（3）的关键是用tan∠DQR=tan∠EQP建立方程，是一道中等难度的题目．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    9．计算：$\sqrt{81}$+$\root{3}{-27}$-$\sqrt{（-5）^{2}}$-|-2$\sqrt{3}$|=1-2$\sqrt{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．函数y=$\frac{k}{x}$与y=-kx2+k（k≠0）在同一直角坐标系中的图象可能是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．$\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$是方程mx+y-1=0的一组解，则m的值是$-\frac{1}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．一元一次方程$\frac{x}{1×3}$+$\frac{x}{3×5}$+$\frac{x}{5×7}$+…+$\frac{x}{2013×2015}$=$\frac{2014}{2015}$的解是（　　）
    A．1B．2C．2014D．2015

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．已知|a|=3，$\sqrt{b}$=2，且ab＜0，则a-b=-7．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．满足下列条件的△ABC中，不是直角三角形的是（　　）
    A．b2=c2-a2B．a：b：c=3：4：5C．∠C=∠A-∠BD．∠A：∠B：∠C=3：4：5

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．对于函数y=xn+xm，我们定义y'=nxn-1+mxm-1（m、n为常数）．
    例如y=x4+x2，则y'=4x3+2x．
    已知：y=$\frac{1}{3}$x3+（m-1）x2+m2x．
    （1）若方程y′=0有两个相等实数根，则m的值为$\frac{1}{2}$；
    （2）若方程y′=m-$\frac{1}{4}$有两个正数根，则m的取值范围为$m≤\frac{3}{4}$且$m≠\frac{1}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．计算
    （1）$\frac{3}{\sqrt{3}}$-（$π+\sqrt{3}$）0+$\sqrt{3}$-|$\sqrt{3}$-2|
    （2）（1-$\sqrt{5}$）（$\sqrt{5}$+1）+（$\sqrt{5}$-1）2
    （3）$\sqrt{48}$-$\sqrt{54}$÷2+（3-$\sqrt{3}$）（1+$\frac{1}{\sqrt{3}}$）
    （4）（3$\sqrt{12}$-2$\sqrt{\frac{1}{3}}$+$\sqrt{48}$）$÷2\sqrt{3}$．

    查看答案和解析>>

    同步练习册答案