
【题目】小明拿两个大小不等直角三角板作拼图,如图①小三角板的斜边与大三角板直角边正好重合,已知:AD=1,∠B=∠ACD=30°.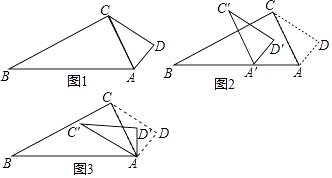
(1)AB的长;四边形ABCD的面积=(直接填空);
(2)如图2,若小明将小三角板ACD沿着射线AB方向平移,设平移的距离为m(平移距离指点A沿AB方向锁经过的线段长度),当点D平移到线段大三角板ABC的边上时,求出相应的m的值;
(3)如图3,小明将小三角板ACD绕点A顺时针旋转一个角α(0°<α<180°),记旋转中的△ACD为△AC′D′,在旋转过程中,设C′D′所在的直线与直线BC交于点P,与直线AB交于点Q,是否存在这样的P、Q两点,使△BPQ为等腰三角形?若存在,请直接求出此时D′Q的长;若不存在,请说明理由
【答案】
(1)4,![]()
(2)解:如图2中,作DE∥AB交BC于E,交AC于F.
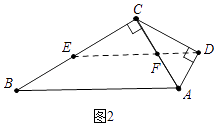
∴∠DFA=∠BAC=60°=∠DAF,
∴△ADF是等边三角形,
∴AF=AD=DF=CF=1,∵FE∥AB,
∴CE=EB,
∴EF= ![]() AB=2,
AB=2,
∴当点D平移到线段大三角板ABC的边上时,相应的m的值为1或3.
(3)解:①如图3中,当BP=BQ时,在AD′上取一点E使得AE=EQ.
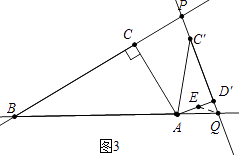
∵∠PBQ=30°,
∴∠AQD′=75°,∵∠AD′Q=90°,
∴∠EAQ=∠EQA=15°
∴∠QED′=30°,设D′Q=x,则AE=EQ=2x,ED′= ![]() x,
x,
∴2x+ ![]() x=1,
x=1,
∴x=2﹣ ![]() ,
,
∴D′Q=2﹣ ![]() .
.
②如图4中,当BQ=PQ时,易知∠AQD′=60°,D′Q=ADtan30°= ![]() .
.
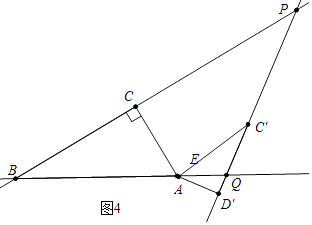
③如图5中,当BP=BQ时,易知∠AQC′=∠C′AQ=15°,∴AC′=C′Q,∴D′Q=D′C+C′Q′= ![]() +2.
+2.
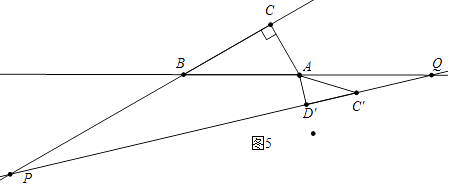
综上所述,当△PBQ是等腰三角形时,D′Q的值为2﹣ ![]() 或
或 ![]() 或
或 ![]() +2
+2
【解析】解:(1)如图1中,
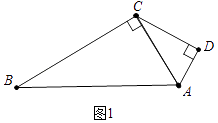
在Rt△ACD中,∵AD=1,∠ACD=30°,
∴AC=2CD=2,CD= ![]() AD=
AD= ![]() ,
,
在Rt△ACB中,∵∠B=30°,AC=2,
∴AB=2AC=4,BC= ![]() AC=2
AC=2 ![]() ,
,
∴四边形ABCD的面积=S△ACD+S△ABC= ![]() +
+ ![]() 22
22 ![]() =
= ![]() .
.
所以答案是4, ![]() .
.
【考点精析】解答此题的关键在于理解含30度角的直角三角形的相关知识,掌握在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半,以及对平行线分线段成比例的理解,了解三条平行线截两条直线,所得的对应线段成比例.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】抗震救灾中,某县粮食局为了保证库存粮食的安全,决定将甲、乙两个仓库的粮食,全部转移到具有较强抗震功能的A、B两仓库.已知甲库有粮食100吨,乙库有粮食80吨,而A库的容量为70吨,B库的容量为110吨.从甲、乙两库到A、B两库的路程和运费如下表:(表中“元/吨千米”表示每吨粮食运送1千米所需人民币)
路程(千米) | 运费(元/吨千米) | |||
甲库 | 乙库 | 甲库 | 乙库 | |
A库 | 20 | 15 | 12 | 12 |
B库 | 25 | 20 | 10 | 8 |
(1)若甲库运往A库粮食x吨,请写出将粮食运往A、B两库的总运费y(元)与x(吨)的函数关系式;
(2)当甲、乙两库各运往A、B两库多少吨粮食时,总运费最省,最省的总运费是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学举行十佳歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.
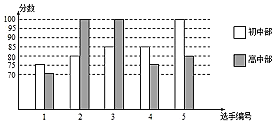
(1)根据所给信息填空:
平均数(分) | 中位数(分) | 众数(分) | 方差 | |
初中部 | 85 | ______ | 85 | _______ |
高中部 | _____ | 80 | ______ | 160 |
(2)你觉得高中部和初中部的决赛成绩哪个更好?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,把矩形OCBA绕点C顺时针旋转α角,得到矩形FCDE,设FC与AB交于点H,且A(0,4),C(6,0).
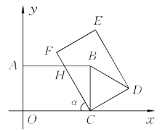
(1)当α=45°时,求H点的坐标.
(2)当α=60°时,ΔCBD是什么特殊的三角形?说明理由.
(3)当AH=HC时,求直线HC的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
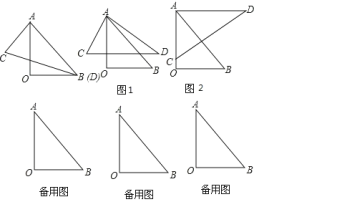
【题目】一副三角板的三个内角分别是90![]() ,45
,45![]() ,45
,45![]() 和90
和90![]() ,60
,60![]() ,30
,30![]() ,按如图所示叠放在一起,若固定三角形AOB,改变三角形ACD的位置(其中点A位置始终不变),可以摆成不同的位置,使两块三角板至少有一组边平行。设∠BAD=α(0
,按如图所示叠放在一起,若固定三角形AOB,改变三角形ACD的位置(其中点A位置始终不变),可以摆成不同的位置,使两块三角板至少有一组边平行。设∠BAD=α(0![]() <α<180
<α<180![]() )
)
(1)如图1中,请你探索当α为多少时,CD∥OB,并说明理由;
(2)如图2中,当α=___时,AD∥OB;
(3)在点A位置始终不变的情况下,你还能摆成几种不同的位置,使两块三角板中至少有一组边平行,请直接写出符合要求的α的度数。(写出三个即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个单位为1的方格纸上,△A1A2A3 , △A3A4A5 , △A5A6A7 , …,是斜边在x轴上、斜边长分别为2,4,6,…的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,﹣1),A3(0,0),则依图中所示规律,A2017的横坐标为( )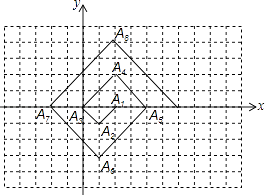
A.1010
B.2
C.1
D.﹣1006
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个点在第一,四象限及x轴上运动,在第1次,它从原点运动到点(1,﹣1),用了1秒,然后按图中箭头所示方向运动,即(0,0)→(1,﹣1)→(2,0)→(3,1)→…,它每运动一次需要1秒,那么第2020秒时点所在的位置的坐标是__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四个全等的直角三角形按图示方式围成正方形ABCD,过各较长直角边的中点作垂线,围成面积为![]() 的小正方形EFGH,已知AM为Rt△ABM较长直角边,AM=
的小正方形EFGH,已知AM为Rt△ABM较长直角边,AM=![]() EF,则正方形ABCD的面积为( )
EF,则正方形ABCD的面积为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注.某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.请根据统计图中所提供的信息解答下列问题:
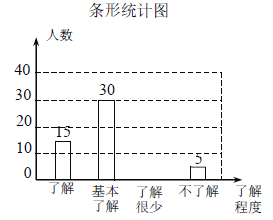
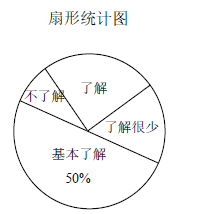
(1)接受问卷调查的学生共有 人;
(2)扇形统计图中“了解”部分所对应扇形的圆心角为 度;
(3)请补全条形统计图;
(4)若该中学共有学生1200人,则该中学学生对校园安全知识达到“了解”和“基本了解”程度的总人数约为多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com