分析:(1)先设P
1(x,y),A
1(x,y'),B
1(x',y),得出x'y=1,xy'=1,再根据
S△OB1D1=
OD
1•B
1D
1=
×y•x',
S△OA1E1=
OE
1•A
1E
1=
y'•x,
S矩形OE1P 1D1=OD
1•OE
1=y•x,最后根据S
1=
S矩形OE1P 1D1-
S△OB1D1-
S△OA1E1代入计算即可;
(2)由(1)同理即可得出四边形P
2A
2OB
2的面积;
(3)先设P
n(x,y),A
n(x,y'),B
n(x',y),根据点A
n,B
n在反比例函数
yn-1=图象上,得出S
△OBnDn=
OD
n•B
nD
n=
×y•x'=
(n-1),
S△OAnEn=
OE
n•A
nE
n=
y'•x=
(n-1),
根据点P
n在反比例函数
yn=上,得出xy=n,再根据
S矩形OEnP nDn=OD
n•OE
n=y•x=n,最后根据S
n=
S矩形OEnP nDn-
S△OBnDn-
S△OAnEn代入计算即可.
解答:解:(1)设P
1(x,y),A
1(x,y'),B
1(x',y),则OE
1=x,OD
1=y,A
1E
1=y',B
1D
1=x',
∵点A
1,B
1在反比例函数
y1=图象上,
∴x'y=1,xy'=1,
∴
S△OB1D1=
OD
1•B
1D
1=
×y•x'=
,
S△OA1E1=
OE
1•A
1E
1=
y'•x=
,
∵点P
1在反比例函数
y2=上,
∴xy=2,
∴
S矩形OE1P 1D1=OD
1•OE
1=y•x=2,
∴S
1=
S矩形OE1P 1D1-
S△OB1D1-
S△OA1E1=2-
-=1;
(2)由(1)同理可得,四边形P
2A
2OB
2的面积S
2=1,
故答案为:1
(3)设P
n(x,y),A
n(x,y'),B
n(x',y),则OE
n=x,OD
n=y,A
nE
n=y',B
nD
n=x',
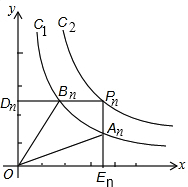
∵点A
n,B
n在反比例函数
yn-1=图象上,
∴x'y=n-1,xy'=n-1,
∴S
△OBnDn=
OD
n•B
nD
n=
×y•x'=
(n-1),
S△OAnEn=
OE
n•A
nE
n=
y'•x=
(n-1),
∵点P
n在反比例函数
yn=上,
∴xy=n,
∴
S矩形OEnP nDn=OD
n•OE
n=y•x=n,
∴S
n=
S矩形OEnP nDn-
S△OBnDn-
S△OAnEn=n-
(n-1)
-(n-1)=1;
点评:此题考查了反比例函数的综合应用,解题的关键是掌握反比例函数的解析式与三角形的面积和矩形的面积之间的关系,同时要注意运用数形结合的思想.





 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案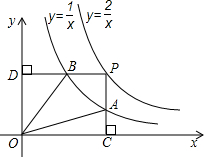 如图,两个反比例函数y=
如图,两个反比例函数y=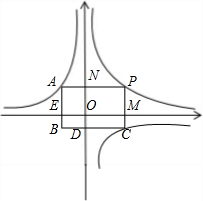 如图,两个反比例函数y=
如图,两个反比例函数y= (2012•德州)如图,两个反比例函数y=
(2012•德州)如图,两个反比例函数y= 如图,两个反比例函数y=
如图,两个反比例函数y=