
【题目】在△ABC中,AB=AC,点D在边BC上,点E在边AC上,且AD=AE.
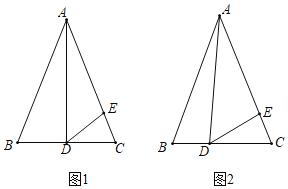
(1)如图1,当AD是边BC上的高,且∠BAD=30°时,求∠EDC的度数;
(2)如图2,当AD不是边BC上的高时,请判断∠BAD与∠EDC之间的关系,并加以证明.
【答案】(1)15°;(2)∠BAD=2∠EDC,证明详见解析.
【解析】
(1)由AD是边BC上的高,得到∠ADC=90°,根据等腰三角形的性质即可得到结论;
(2)根据等腰三角形的性质得到∠B=∠C,∠ADE=∠AED,根据三角形外角的性质得到∠ADC=∠B+∠BAD,∠AED=∠C+∠EDC,于是得到结论.
(1)∵AD是边BC上的高,
∴∠ADC=90°,
∵AB=AC,
∴AD是∠BAC的角平分线,
∴∠BAD=∠CAD,
∵∠BAD=30°,
∴∠CAD=30°,
∵AD=AE,
∴∠ADE=∠AED=75°,
∴∠EDC=∠ADC﹣∠ADE=90°﹣75°=15°;
(2)∠BAD=2∠EDC,
理由:∵AB=AC,AD=AE,
∴∠B=∠C,∠ADE=∠AED,
∵∠ADC=∠B+∠BAD,∠AED=∠C+∠EDC,
∴∠B+∠BAD=∠ADC=∠ADE+∠EDC=∠AED+∠∠EDC=∠C+2∠EDC,
∴∠BAD=2∠EDC.


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)和点B,与y轴交于C(0,3),直线y=![]() +m经过点C,与抛物线的另一交点为点D,点P是直线CD上方抛物线上的一个动点,过点P作PF⊥x轴于点F,交直线CD于点E,设点P的横坐标为m.
+m经过点C,与抛物线的另一交点为点D,点P是直线CD上方抛物线上的一个动点,过点P作PF⊥x轴于点F,交直线CD于点E,设点P的横坐标为m.
(1)求抛物线解析式并求出点D的坐标;
(2)连接PD,△CDP的面积是否存在最大值?若存在,请求出面积的最大值;若不存在,请说明理由;
(3)当△CPE是等腰三角形时,请直接写出m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过
经过![]() 、
、![]() 两点.
两点.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 如图,点
如图,点![]() 是直线
是直线![]() 上方抛物线上的一动点,当
上方抛物线上的一动点,当![]() 面积最大时,请求出点
面积最大时,请求出点![]() 的坐标和
的坐标和![]() 面积的最大值?
面积的最大值?
![]() 在
在![]() 的结论下,过点
的结论下,过点![]() 作
作![]() 轴的平行线交直线
轴的平行线交直线![]() 于点
于点![]() ,连接
,连接![]() ,点
,点![]() 是抛物线对称轴上的动点,在抛物线上是否存在点
是抛物线对称轴上的动点,在抛物线上是否存在点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形?如果存在,请直接写出点
为顶点的四边形是平行四边形?如果存在,请直接写出点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了预防“流感”,某学校对教室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量![]() 与时间
与时间![]() 成正比例,药物燃烧完后,
成正比例,药物燃烧完后,![]() 与
与![]() 成反比例(如图所示).现测得药物
成反比例(如图所示).现测得药物![]() 燃毕,此时室内空气中每立方米的含药量为
燃毕,此时室内空气中每立方米的含药量为![]() .研究表明,当空气中每立方米的含药量不低于
.研究表明,当空气中每立方米的含药量不低于![]() 才有效,那么此次消毒的有效时间是( )
才有效,那么此次消毒的有效时间是( )

A. ![]() 分钟 B.
分钟 B. ![]() 分钟 C.
分钟 C. ![]() 分钟 D.
分钟 D. ![]() 分钟
分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在正方形网格上有6个三角形:①△ABC;②△BCD;③△BDE;④△BFG;⑤△FGH;⑥△EFK.其中②~⑥中与①相似的是( )

A. ②③④ B. ③④⑤ C. ④⑤⑥ D. ②③⑥
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程:x2﹣2(m+1)x+m2+5=0有两个不相等的实数根.
(1)求m的取值范围;
(2)若原方程的两个实数根为x1、x2, 且满足x12+x22=|x1|+|x2|+2x1x2,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售某种玩具,进货价为![]() 元.根据市场调查:在一段时间内,销售单价是
元.根据市场调查:在一段时间内,销售单价是![]() 元时,销售量是
元时,销售量是![]() 件,而销售单价每上涨
件,而销售单价每上涨![]() 元,就会少售出
元,就会少售出![]() 件玩具,超市要完成不少于
件玩具,超市要完成不少于![]() 件的销售任务,又要获得最大利润,则销售单价应定为________元.
件的销售任务,又要获得最大利润,则销售单价应定为________元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com