
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�O������ԭ�㣬������OACB�Ķ���A��B�ֱ���x����y���ϣ���֪OA=3��OB=5����DΪy����һ�㣬������Ϊ��0��1������P�ӵ�A������ÿ��1����λ���ٶ����߶�AC��CB�ķ����˶�������P���B�غ�ʱֹͣ�˶����˶�ʱ��Ϊt�룮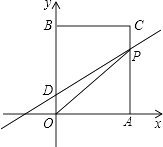
��1������P������Cʱ����ֱ��DP�ĺ�������ʽ��
��2�������OPD�����S����t�ĺ�������ʽ��
�ڵ���D����OP�ĶԳƵ�����x����ʱ�����P�����꣮
��3����P���˶��������Ƿ����ʹ��BDPΪ���������Σ������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺���ʱֱ��DP����ʽΪy=kx+b��
��D��0��1����C��3��5������ã� ![]() ��
��
��ã� ![]() ��
��
���ʱֱ��DP����ʽΪy= ![]() x+1
x+1
��2��
�⣺�ٵ���P���߶�AC��ʱ��OD=1����Ϊ3��S= ![]() ��
��
����P���߶�BC��ʱ��OD=1����Ϊ3+5��t=8��t��S= ![]() ��1����8��t��=��
��1����8��t��=�� ![]() t+4��
t+4��
�ڵ���D����OP�ĶԳƵ�����x����ʱ��D�ԳƵ�Ϊ��1��0������ʱֱ��OPΪy=x��
���ʱ��P�������ǣ�3��3��
��3��
�⣺���ڣ�����Ϊ��
����BDPΪ���������Σ�������������ǣ�
�ٵ�BD=BP1=OB��OD=5��1=4��
��Rt��BCP1��BD=4��BC=3��
���ݹ��ɶ����ã�CP1= ![]() =
= ![]() ��
��
��AP1=5�� ![]() ����P1��3��5��
����P1��3��5�� ![]() ����
����
�ڵ�BP2=DP2ʱ����ʱP2��3��3����
�۵�DB=DP3=4ʱ��
��Rt��DEP3��DE=3��
���ݹ��ɶ����ã�P3E= ![]() =
= ![]() ��
��
��AP3=AE+EP3= ![]() +1����P3��3��
+1����P3��3�� ![]() +1����
+1����
���ϣ����������P����Ϊ��3��3����3�� ![]() +1����3��5��
+1����3��5�� ![]() ����
����

����������1����ֱ��DP����ʽΪy=kx+b����D��B����������k��b��ֵ������ȷ��������ʽ����2���ٵ�P��AC��ʱ��������ODP��OD���Ϊ�̶�ֵ�������ʱ�������P��BC��ʱ���ױ�ODΪ�̶�ֵ����ʾ���ߣ������г�S��t�Ĺ�ϵʽ���ڵ�D����OP�ĶԳƵ�����x����ʱ��ֱ��OPΪy=x�������ʱP���꼴�ɣ���3�����ڣ��ֱ���BD��DP��BPΪ�ױ�����������ǣ����ù��ɶ�����ͼ���������������P���꼴�ɣ�
�����㾫����������Ҫ������һ�κ��������ʺ�һ�κ�����ͼ������ʵ����֪ʶ�㣬��Ҫ����һ��أ�һ�κ���y=kx+b���������ʣ���1����k>0ʱ��y��x�����������2����k<0ʱ��y��x���������С��һ�κ�����ֱ�ߣ�ͼ�������ޣ���������������,����ԭ��һֱ�ߣ�����ϵ��k��b,����֮��ĪС����k��б�ʶ��н�,b��Y�������,kΪ��������б,x����y������kΪ��������չ,�仯�������෴��k�ľ���ֵԽ��,��������ԽԶ������ȷ�����⣮


 �����ѧСѧ�꼶�νӽݾ��㽭��ѧ������ϵ�д�
�����ѧСѧ�꼶�νӽݾ��㽭��ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һԪ���η���x2��2x��1��0�������б�ʽb2��4ac�е�b��ʾ�����ǣ� ��
A.��2B.2C.��1D.1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(10��)��ͼ���ҹ��������ڵ��㵺����C����õ��㵺A���������ı�ƫ��30���ķ����ϣ������������80����/Сʱ���ٶ���ƫ��30��ķ����У���Сʱ��B������ʱ�ֲ�õ��㵺A���������ı�ƫ��60��ķ����ϣ����ʱ����������㵺A�ľ�����B.(�������С�����һλ������![]() 1.732)
1.732)
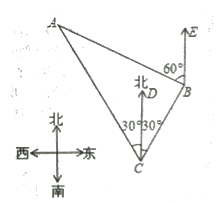
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijһ�߳��жԳ��Ӫ�˼۽����˵���������ǰ����շѱ��Ա�����:����ǰ,3���P3��������12.5Ԫ��3�������̼�2.4Ԫ/������շѣ�������, 2���P2��������10Ԫ��2�������̼�2.4Ԫ/�������25���ﲿ�֣�����̼۵�30%���շ��շѣ�
��1�������æ����һ�£����ۺ����˿ͳ���������г�Ϊ8���������ǰ�ٸ��˶���Ǯ�������Ǻ�Ƶ����أ���
��2������������24���ﻻ������ܷ��շѣ����˿͵��г̳���25�������24���ﴦ�³���������һ�����������ʵ�����������г̳���25����ij˿Ͷ���Ҫ������
���磺�����г�Ϊ30������������ܷ���Ϊ��
10+23��2.4+5��2.4��130%=80.8Ԫ��
�������ܷ���Ϊ��10+22��2.4+10+4��2.4��82.4Ԫ����ˣ��г�30����������������÷�������2.4Ԫ��
�����г�Ϊ40������������ܷ���Ϊ��
10+23��2.4+15��2.4��130%=112Ԫ�����������ܷ���Ϊ��10+22��2.4+10+2.4��14��106.4Ԫ����ɽ�Լ5.6Ԫ��
�����г�Ϊx ���26��x��48 �������ú�x��ʽ�ӷֱ��ʾ���������ķ��úͻ����ķ��ã�����æ����һ�£��г̳������ٹ������ͻ��Լ���ã������Ǻ�Ƶ����أ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾����ijһ������ͨѶ��Ʒ����֪ÿ����Ʒ�Ľ���Ϊ4��Ԫ��ÿ�����۸��ֲ�Ʒ���ܿ�֧(��������)�ܼ�11��Ԫ.�����۹����з��֣���������Ϧ(��)�����۵���x (��Ԫ)֮���������ͼ��ʾ��һ�κ�����ϵ��
(1)��y����x�ĺ�����ϵʽ(ֱ��д�����)
(2)��д���ù�˾���۸��ֲ�Ʒ���»���z(��Ԫ)�������۵���x(��Ԫ)�ĺ�����ϵʽ�������۵���xΪ��ֵʱ���»������?����������ֵ(�»���һ�����۶�һ�����۲�Ʒ�ܽ���һ���ܿ�֧)
(3)����˾ϣ���ò�Ʒһ���µ����ۻ���������5��Ԫ������(2)�к�����ͼ����������ù�˾ȷ�����۵��۵ķ�Χ.�ڴ�����£�Ҫʹ��Ʒ�������������Ϊ���۵���Ӧ��Ϊ������Ԫ

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУһ��5��Ľ�ѧ��¥����һ��û�н��ң�������㣬ÿ��¥��6����ң������ⶰ��¥����������С��ͬ�Ĵ��ź�һ��С�ţ�ƽʱС�Ų���������ȫ����У�����3���Ž����˲��ԣ���ͬʱ����һ�����ź�һ��С��ʱ��3�����ڿ���ͨ��540��ѧ������һ������ƽ��ÿ���ӱ�һ��С�ſɶ�ͨ��60��ѧ����
��1����ƽ��ÿ����һ�����ź�һ��С�Ÿ�����ͨ��������ѧ����
��2������з��֣��������ʱ��ѧ��ӵ�������ŵ�Ч�ʽ���20%����ȫ���涨���ڽ��������ȫ��¥��ѧ��Ӧ��5�����ڰ�ȫ���룮�ⶰ��ѧ��¥ÿ�����ƽ����45��ѧ�����ʣ��ڽ��������ֻ�������������Ƿ���У�Ϊʲô��3���Ŷ������أ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�����һ�ֳɱ�Ϊ50Ԫ/����![]() �������������֣�������
�������������֣�������![]() �����������۵���
�����������۵���![]() ��Ԫ/��������һ�κ�����ϵ�������������±���
��Ԫ/��������һ�κ�����ϵ�������������±���
�ۼۣ�Ԫ/���� | ���� | 55 | 60 | 70 | ���� |
���������� | ���� | 75 | 70 | 60 | ���� |
��1����һ�κ���![]() �ı���ʽ��
�ı���ʽ��
��2�������̳��������ΪWԪ����д������W�����۵���![]() ֮��Ĺ�ϵʽ�����۵��۶�Ϊ����ʱ���̳��ɻ�����������������Ƕ��٣�
֮��Ĺ�ϵʽ�����۵��۶�Ϊ����ʱ���̳��ɻ�����������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������������õ��Ľ�����˵����ȷ���ǣ� ��
A.0.720��ȷ���ٷ�λ
B.5.078��104��ȷ��ǧ��λ
C.3.6��ȷ��ʮ��λ
D.2.90��ȷ��0.01
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м�����ȷ���ǣ� ��
A.a2+a2=a4
B.��a2��3=a5
C.a+2=2a
D.��ab��3=a3b3
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com