

分析 (1)由矩形的性质和勾股定理求出OC,即可得出结果;
(2)根据题意和菱形的性质、勾股定理得出方程,解方程求出CD,得出AE的长和点E、D的坐标,用待定系数法求出直线DE的解析式即可;
(3)分三种情况:①当OE=OC时;②当OE=CE时;③当CE=OC时;根据勾股定理得出方程,解方程即可.
解答 解:(1)∵A(0,3),AC=5,
∴OC=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴B(4,3),C(4,0);
(2)存在,在整个运动过程中,所形成的四边形AECD可能是菱形,如图1所示: ∵E、D运动速度相同,又是同时出发,
∵E、D运动速度相同,又是同时出发,
若CD=AE,则四边形AECD为平行四边形,
又若AE=CE时,即CD=CE,?AECD是菱形,
设运动t秒,四边形AECD是菱形,
则CD=t,CE2=BE2+BC2=(4-t)2+32,
∵CD2=CE2,
∴t2=(4-t)2+9,
解得:t=$\frac{25}{8}$,
∴AE=$\frac{25}{8}$×1=$\frac{25}{8}$,
此时E($\frac{25}{8}$,3),D(4-$\frac{25}{8}$,0)即($\frac{7}{8}$,0),
设直线DE的解析式为y=kx+b(k≠0),
根据题意得:$\left\{\begin{array}{l}{\frac{25}{8}k+b=3}\\{\frac{7}{8}k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{4}{3}}\\{b=-\frac{7}{6}}\end{array}\right.$,
∴yDE=$\frac{4}{3}$x-$\frac{7}{6}$;
(3)存在某一时刻t,使△OCE为等腰三角形,如图2所示:
分三种情况:
①当OE=OC时,AE=t,OA=3,OC=4,
则OE2=t2+32,
∴42=t2+32,t2=7,
解得:t=$\sqrt{7}$(s),
∴E($\sqrt{7}$,3);
②当OE=CE时,OE2=t2+32,CE2=(4-t)2+32,
∴t2+32=(4-t)2+32,
解得:t=2(s),
∴E(2,3);
③当CE=OC时,CE2=(4-t)2+32,OC=4,
∴42=(4-t)2+32,
∴t2-8t+9=0,
解得:t=4±$\sqrt{7}$,
∵点E运动到B点时停止运动,此时用了$\frac{4}{1}$=4(s),
∵4+$\sqrt{7}$>4,不合题意舍去,
∴t=4-$\sqrt{7}$(s),
∴E(4-$\sqrt{7}$,3);
综上所述,E点的坐标为($\sqrt{7}$,3)或(2,3)或(4-$\sqrt{7}$,3).
点评 本题是四边形综合题目,考查了矩形的性质、勾股定理、用待定系数法求直线的解析式、菱形的判定与性质、等腰三角形的判定与性质等知识;本题难度较大,综合性强,特别是(3)中,需要进行分类讨论,根据勾股定理得出方程才能得出结果.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
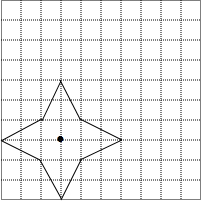 如图,一朵四瓣花飘动在10×10的网格中.
如图,一朵四瓣花飘动在10×10的网格中.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,等腰三角形ABC中,∠BAC=90°,AB=AC,点D在BC上,点F在AD上,过点F作EG⊥AD,交AB于E,AC于G,猜测AE,AG,BD,BC之间是否成比例,并说明理由.
如图,等腰三角形ABC中,∠BAC=90°,AB=AC,点D在BC上,点F在AD上,过点F作EG⊥AD,交AB于E,AC于G,猜测AE,AG,BD,BC之间是否成比例,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com