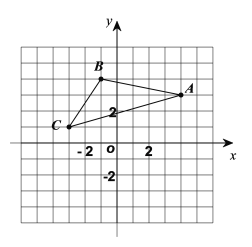
[题目]如图.在△ABC中.A点坐标为(4.3).B点坐标为(-1.4).C点坐标为(-3.1)．(1)在图中画出△ABC关于x轴对称的△A′B′C′.并写出点A′.B′.C′的坐标．(2)在x轴上画出点P.使PA+PC最小．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】如图，在△ABC中，A点坐标为（4，3），B点坐标为（－1，4），C点坐标为（－3，1）．

（1）在图中画出△ABC关于x轴对称的△A′B′C′（不写画法），并写出点A′，B′，C′的坐标．

（2）在x轴上画出点P，使PA+PC最小．

【答案】（1）见详解；（2）见详解

【解析】

（1）根据网格结构找出点A′、B′、C′的位置，然后顺次连接即可；

（2）作点C关于x轴的对称点C′，连接AC′交x轴于P，此时PA+PC最短．PA+PC的最小值=PC′．

解：（1）△ABC关于x轴对称的△A′B′C′如图所示．

A′，B′，C′的坐标分别为：（4，-3），（－1，-4），（－3，-1）

（2）作点C关于x轴的对称点C′，连接AC′交x轴于P，此时PA+PC最短．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

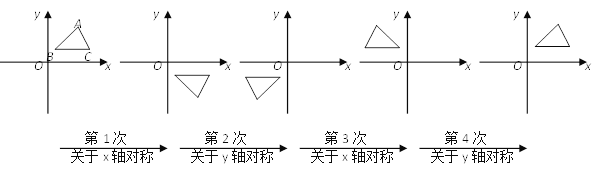
【题目】如图，在平面直角坐标系中，对△ABC进行循环往复的轴对称变换，若原来点A坐标是（2，3），则经过第2018次变换后所得的A点坐标是________．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图,在长方形纸片中, ,折叠纸片,使得点落在边上的点处,折痕为,点分别在边和上,当点恰好是边的中点时,点与点重合,若在折叠过程中,则等于________.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，在△ABC中，AB＝AC，D，E是△ABC内的两点，AD平分∠BAC，∠EBC＝∠E＝60°．若BE＝9cm，DE＝3cm，则BC的长为（　　）

A.12cmB.11cmC.9cmD.6cm

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】（1）问题发现

如图1，△ABC和△DCE都是等边三角形，点B、D、E在同一直线上，连接AE．

填空：

①∠AEC的度数为　　；

②线段AE、BD之间的数量关系为　　．

（2）拓展探究

如图2，△ABC和△DCE都是等腰直角三角形，∠ACB=∠DCE=90°，点B、D、E在同一直线上，CM为△DCE中DE边上的高，连接AE．试求∠AEB的度数及判断线段CM、AE、BM之间的数量关系，并说明理由．

（3）解决问题

如图3，在正方形ABCD中，CD=2，点P在以AC为直径的半圆上，AP=1，①∠DPC=　 °； ②请直接写出点D到PC的距离为　．

查看答案和解析>>

科目：初中数学 来源： 题型：

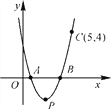
【题目】如图，抛物线y＝ax2－5ax＋4a与x轴相交于点A，B，且过点C(5，4)．

(1)求a的值和该抛物线顶点P的坐标；

(2)请你设计一种平移的方法，使平移后抛物线的顶点落在第二象限，并写出平移后抛物线的表达式．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，△ABC为直角三角形，∠C=90°，BC=2cm，∠A=30°，四边形DEFG为矩形，DE=2cm，EF=6cm，且点C、B、E、F在同一条直线上，点B与点E重合．Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移，当点C与点F重合时停止．设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2，运动时间xs．能反映ycm2与xs之间函数关系的大致图象是（　　）

A. B. C. D.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】“网络红包”是互联网运营商、商家通过组织互联网线上活动、派发红包的互联网工具，是朋友间互道祝福的表达形式之一．“网络红包”春节活动已经逐渐深入到大众的生活中，得到了人们较为广泛的关注．根据某咨询公司（2018年中国春节“网络红包”专题调查报告》显示：在接受调查的8万名网民中，对“网络红包”春节话动了解程度的占比方面，“较为了解”和“很了解”的网民共占比64%，分别占比36%和28%．在“不了解”和“只了解一两个“的受访网民中，“不了解”的网民人数比“只了解一两个”的网民人数多25%．如图是该咨询公司绘制的“中国网民关于‘网络红包’春节活动了解情况调查”统计图（不完整）．

请根据以上信息解答下列问题：

（1）在受访的网民中，“不了解”和“只了解一两个”的网民人数共有　　万人，其中“不了解”的网民人数是　　万人；

（2）请将扇形统计图补充完整；

（3）2017除夕晚上小聪和爸爸、妈妈一起玩微信抢红包游戏，他们约定由爸爸在家人微信群中先后发两次“拼手气红包”，每次发放的红包数是3个，每个红包抽到的金额随机（每两个红包的金额都不相等），每次谁抽到红包的金额最大谁就是“手气最佳”者，求两次游戏中小聪都能获得“手气最佳”的概率为多少？