
【题目】如图![]() 中,
中,![]() ,P是斜边AC上一个动点,以即为直径作
,P是斜边AC上一个动点,以即为直径作![]() 交BC于点D,与AC的另一个交点E,连接DE.
交BC于点D,与AC的另一个交点E,连接DE.
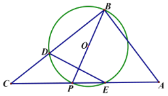

(1)当![]() 时,
时,
①若![]() ,求
,求![]() 的度数;
的度数;
②求证![]() ;
;
(2)当![]() ,
,![]() 时,
时,
①是含存在点P,使得![]() 是等腰三角形,若存在求出所有符合条件的CP的长;
是等腰三角形,若存在求出所有符合条件的CP的长;
②以D为端点过P作射线DH,作点O关于DE的对称点Q恰好落在![]() 内,则CP的取值范围为________.(直接写出结果)
内,则CP的取值范围为________.(直接写出结果)
【答案】(1)①40°;②详见解析;(2)①7,10,12.5;②![]()
【解析】
(1)①由BP是直径可得![]() ,根据
,根据![]() 得
得 ![]() 并可得
并可得![]() ,
, ![]() ,
,![]() ,根据三角形的内角和定理得
,根据三角形的内角和定理得![]() ;②由
;②由![]() ,得到
,得到![]() ,根据
,根据![]() ,
,![]() ,
,![]() ,得到,
,得到,![]() 由等角对等边得
由等角对等边得![]() ;
;
(2)①分三种情况:(一)当![]() 时,(二)当
时,(二)当![]() 时,(三)当
时,(三)当![]() 时,分别进行讨论求解即可;
时,分别进行讨论求解即可;
②分三种情况讨论:(一)当Q点在P点上时;(二)当Q点在PC上时(三)当Q点在PH上时,分别讨论,求出CP的值即可.
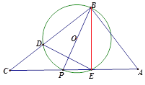
24.解(1)①连结BE,∵BP是直径∴![]()

∵![]() ,∴
,∴![]()
∵![]() ,∴
,∴![]() ∴
∴![]()
∴![]()
②∵![]() ,∴
,∴![]()
![]() ,
,![]()
又∵![]()
∴![]()
∴![]()
(2)①由![]() ,
,![]() ,可以求得
,可以求得![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,![]()
∴![]()
当![]() 是等腰三角形时,有三种情况:(一)
是等腰三角形时,有三种情况:(一)![]() ,(二)
,(二)![]() ,(三)
,(三)![]()
(一)当![]() 时,
时,![]()
∴![]() ,
,
∴![]()
∴![]()
(二)当![]() 时,可知点D是
时,可知点D是![]() 斜边的中线,
斜边的中线,
∴![]() ,
,
∴![]()
∴![]()
(三)当![]() 时,
时,

作![]() ,则H是BD中点,
,则H是BD中点,
可以求得![]() ,∴
,∴![]()
∴![]() ,∴
,∴![]()
②(一)当O点的对称点Q在P点上时,B,O,Q三点共线,
如图示

∴![]() ,且BP平分DE,由等腰三角形的性质可知
,且BP平分DE,由等腰三角形的性质可知
∴![]()
由(1)可知CP=7;
(二)当O点的对称点Q不在P点上,而在PC上时,此情况Q点并不在![]() 上
上
(三)当O点的对称点Q不在P点上,而在PH上时,B,O,Q三点不共线,
如图示

∵![]() ,
,![]() ,且
,且![]()
∴四边形DOEQ是菱形,
∴![]()
∵![]()
∴![]()
又∵OE,OD,OB均为外接圆的半径,
∴![]() ,
,![]()
∴![]()
∴![]()
∴![]()
∴由(1)可知,![]()
∴![]()


科目:初中数学 来源: 题型:
【题目】在水果销售旺季,某水果店购进一优质水果,进价为20元/千克,售价不低于20元/千克,且不超过32元/千克,根据销售情况,发现该水果一天的销售量y(千克)与该天的售价x(元/千克)满足如下表所示的一次函数关系.
销售量y(千克) | … | 34.8 | 32 | 29.6 | 28 | … |
售价x(元/千克) | … | 22.6 | 24 | 25.2 | 26 | … |
(1)某天这种水果的售价为23.5元/千克,求当天该水果的销售量.
(2)如果某天销售这种水果获利150元,那么该天水果的售价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬传统文化,某校开展了“传承经典文化,阅读经典名著”活动.为了解七、八年级学生(七、八年级各有600名学生)的阅读效果,该校举行了经典文化知识竞赛.现从两个年级各随机抽取20名学生的竞赛成绩(百分制)进行分析,过程如下:
收集数据:
七年级:79,85,73,80,75,76,87,70,75,94,75,79,81,71,75,80,86,59,83,77.
八年级:92,74,87,82,72,81,94,83,77,83,80,81,71,81,72,77,82,80,70,41.
整理数据:
|
|
|
|
|
| |
七年级 | 0 | 1 | 0 | a | 7 | 1 |
八年级 | 1 | 0 | 0 | 7 | b | 2 |
分析数据:
平均数 | 众数 | 中位数 | |
七年级 | 78 | 75 |
|
八年级 | 78 |
| 80.5 |
应用数据:
(1)由上表填空:a= ,b= ,c= ,d= .
(2)估计该校七、八两个年级学生在本次竞赛中成绩在90分以上的共有多少人?
(3)你认为哪个年级的学生对经典文化知识掌握的总体水平较好,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
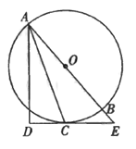
【题目】如图,AB为⊙O的直径,C为⊙O上一点,经过点C的切线交AB的延长线于点E , ![]() 交EC的延长线于点D,连接AC .
交EC的延长线于点D,连接AC .
(1)求证: AC平分∠DAE ;
(2)若![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中,装有2个白球和1个红球,这些球除颜色外都相同.
(1)小明认为,搅匀后从中任意摸出一个球,不是白球就是红球是等可能的,你同意他的说法吗?为什么?
(2)搅匀后从中一把摸出两个球,请通过列表和树状图求出两个球都是白球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用两种方法证明“圆的内接四边形对角互补”.
已知:如图①,四边形ABCD内接于⊙O.
求证:∠B+∠D=180°.
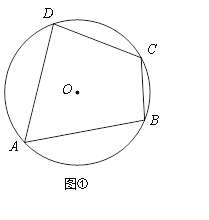

证法1:如图②,作直径DE交⊙O于点E,连接AE、CE.
∵DE是⊙O的直径,
∴ .
∵∠DAE+∠AEC+∠DCE+∠ADC=360°,
∴∠AEC+∠ADC=360°-∠DAE-∠DCE=360°-90°-90°=180°.
∵∠B和∠AEC所对的弧是![]() ,
,
∴ .
∴∠B+∠ADC=180°.
请把证法1补充完整,并用不同的方法完成证法2.
证法2:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AB是⊙O的直径,CE平分∠ACB交⊙O于E,交AB于点D,连接AE,∠E=30°,AC=5.

(1)求CE的长;
(2)求S△ADC:S△ACE的比值.
查看答案和解析>>
科目:初中数学 来源: 题型:
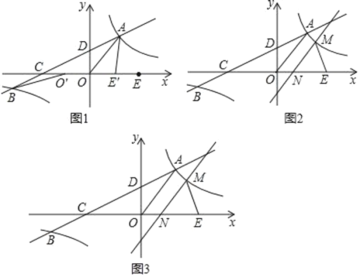
【题目】如图1,在平面直角坐标系xOy中,双曲线![]() 与直线y=ax+b(a≠0)交于A、B两点,直线AB分别交x轴、y轴于C、D两点,E为x轴上一点.已知OA=OC=OE,A点坐标为(3,4).
与直线y=ax+b(a≠0)交于A、B两点,直线AB分别交x轴、y轴于C、D两点,E为x轴上一点.已知OA=OC=OE,A点坐标为(3,4).
(1)将线段OE沿x轴平移得线段O′E′(如图1),在移动过程中,是否存在某个位置使|BO′﹣AE′|的值最大?若存在,求出|BO′﹣AE′|的最大值及此时点O′的坐标;若不存在,请说明理由;
(2)将直线OA沿射线OE平移,平移过程中交![]() 的图象于点M(M不与A重合),交x轴于点N(如图3).在平移过程中,是否存在某个位置使△MNE为以MN为腰的等腰三角形?若存在,求出M的坐标;若不存在,请说明理由.
的图象于点M(M不与A重合),交x轴于点N(如图3).在平移过程中,是否存在某个位置使△MNE为以MN为腰的等腰三角形?若存在,求出M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+![]() x+c交x轴于A,B两点,交y轴于点C.直线y=﹣
x+c交x轴于A,B两点,交y轴于点C.直线y=﹣![]() +2经过点A,C.
+2经过点A,C.
(1)求抛物线的解析式;
(2)点P在抛物线在第一象限内的图象上,过点P作x轴的垂线,垂足为D,交直线AC于点E,连接PC,设点P的横坐标为m.
①当△PCE是等腰三角形时,求m的值;
②过点C作直线PD的垂线,垂足为F.点F关于直线PC的对称点为F′,当点F′落在坐标轴上时,请直接写出点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com