

 ),AB=2(2)①
),AB=2(2)① ②
② (3)y=-
(3)y=- t+
t+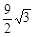 ,y=
,y= 
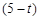 2
2 ),AB=2( 4分)
),AB=2( 4分) ,当
,当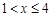 时,
时, (2分)
(2分)
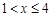 时,
时, ∵-
∵-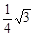 <0 ∴S随x的增大而减小∴S不存在最大值
<0 ∴S随x的增大而减小∴S不存在最大值  (2分)
(2分)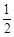 ×(2+3)×
×(2+3)× =
=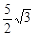
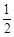 ×(4-t+5-t)×
×(4-t+5-t)× =-
=- t+
t+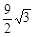
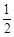 ×
× (5-t)=
(5-t)= 
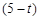 2(4分)
2(4分)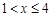 时点到两种不同的结果,然后根据得到的面积表达式为二次函数,利用二次函数的性质得到最值。
时点到两种不同的结果,然后根据得到的面积表达式为二次函数,利用二次函数的性质得到最值。

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:不详 题型:解答题

 千米时(t≥30),求他们经过的时间t的取值范围
千米时(t≥30),求他们经过的时间t的取值范围查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 路线运动,到D停止;点
路线运动,到D停止;点 从
从 出发,沿
出发,沿 路线运动,到
路线运动,到 停止.若点
停止.若点
 同时出发,点
同时出发,点 的速度为
的速度为 点
点 的速度为
的速度为 ,
, 秒时点
秒时点 点
点 同时改变速度,点
同时改变速度,点 的速度变为bcm/s,点
的速度变为bcm/s,点 的速度变为
的速度变为 .图②是点
.图②是点 出发x秒后
出发x秒后 的面积
的面积 与
与 的函数关系图象;图③点
的函数关系图象;图③点 出发
出发 秒后
秒后 的面积
的面积 的函数关系图象.
的函数关系图象. 、c的值及点
、c的值及点 的速度
的速度 的值;
的值; 离开点
离开点 的路程为
的路程为 点
点 到
到 还需走的路程为
还需走的路程为 请分别写出动点
请分别写出动点 改变速度后
改变速度后 与出发后的运动时间
与出发后的运动时间 的函数关系式,并求出
的函数关系式,并求出 相遇时x的值;
相遇时x的值; 出发多少秒时,点
出发多少秒时,点 点
点 在运动路线上相距的路程为25cm.
在运动路线上相距的路程为25cm.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 时,直接写出∠DEF的度数;
时,直接写出∠DEF的度数; ,∠DEF=
,∠DEF= (
( <X<
<X< ,
, <Y<
<Y< ),求:Y关于X的函数解析式及相应自变量X的取值范围,
),求:Y关于X的函数解析式及相应自变量X的取值范围, 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com