
【题目】已知关于x的方程x2﹣2(k﹣1)x+k2=0有两个实数根x1,x2.
(1)求k的取值范围;
(2)若|x1+x2|=x1x2﹣1,求k的值.
【答案】(1)k≤![]() (3分);
(3分);
(2)k=-3(5分
【解析】试题分析:(1)方程有两个实数根,可得△=b2﹣4ac≥0,代入可解出k的取值范围;
(2)结合(1)中k的取值范围,由题意可知,x1+x2=2(k﹣1)<0,去绝对值号结合等式关系,可得出k的值.
解:(1)由方程有两个实数根,可得
△=b2﹣4ac=4(k﹣1)2﹣4k2=4k2﹣8k+4﹣4k2=﹣8k+4≥0,
解得,k≤![]() ;
;
(2)依据题意可得,x1+x2=2(k﹣1),x1x2=k2,
由(1)可知k≤![]() ,
,
∴2(k﹣1)<0,x1+x2<0,
∴﹣x1﹣x2=﹣(x1+x2)=x1x2﹣1,
∴﹣2(k﹣1)=k2﹣1,
解得k1=1(舍去),k2=﹣3,
∴k的值是﹣3.
答:(1)k的取值范围是k≤![]() ;(2)k的值是﹣3.
;(2)k的值是﹣3.


科目:初中数学 来源: 题型:
【题目】如图,已知点E在直角△ABC的斜边AB上,以AE为直径的⊙O与直角边BC相切于点D.
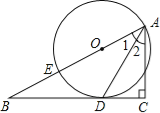
(1)求证:AD平分∠BAC;
(2)若BE=2,BD=4,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面等式成立的是( )
A.83.5°=83°50′
B.37°12′36″=37.48°
C.24°24′24″=24.44°
D.41.25°=41°15′
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com