
分析 ①根据绝对值得出方程x=1,x=-1.
②由-|3x|=1可知|3x|=-1,根据绝对值的性质,此方程无解;
③根据绝对值得出方程x-3=2,x-3=-2,求出方程的解即可.
④根据绝对值得出方程2x+1=5,2x+1=-5,求出方程的解即可.
解答 解:①|x|=1;
当x≥0时,原方程可化为一元一次方程
x=1,它的解是x=1
当x<0时,原方程可化为一元一次方程
-x=1,它的解是x=-1
所以原方程的解是x1=1,x2=-1;
②-|3x|=1;
|3x|=-1,
所以原方程无解;
③|x-3|=2
当x-3≥0时,原方程可化为一元一次方程
x-3=2,它的解是x=5,
当x-3<0时,原方程可化为一元一次方程
3-x=2,它的解是x=1
所以原方程的解是x1=5,x2=1;
④|2x+1|=5,
当2x+1≥0时,原方程可化为一元一次方程
2x+1=5,它的解是x=2,
当2x+1<0时,原方程可化为一元一次方程
2x+1=-5,它的解是x=-3
所以原方程的解是x1=2,x2=-3.
点评 本题考查了解绝对值方程的应用,关键是能根据绝对值的意义得出两个一元一次方程.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:填空题
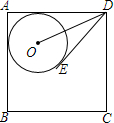 如图,⊙O与正方形ABCD的两边AB、AD相切,且DE与⊙O相切于E点.若正方形ABCD的周长为28,且DE=4,则sin∠ODE=$\frac{3}{5}$.
如图,⊙O与正方形ABCD的两边AB、AD相切,且DE与⊙O相切于E点.若正方形ABCD的周长为28,且DE=4,则sin∠ODE=$\frac{3}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABD、△AEC都是等边三角形.AB、CD相交于M,AC、BE相交于N,∠MAN=60°.求证:
如图,△ABD、△AEC都是等边三角形.AB、CD相交于M,AC、BE相交于N,∠MAN=60°.求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
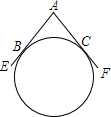 一个圆形工件与两条直尺AE、AF按如图所示的方式放置在一起,所成的夹角为∠EAF=120°,设圆形工件分别与AE、AF相切于点B、C.小明想用刻度尺测量这个圆形工件的直径,但发现刻度尺的长度稍短些.请你设计两种不同的测量方法,仍用这把刻度尺并结合简单的计算,测出这个工件的直径.
一个圆形工件与两条直尺AE、AF按如图所示的方式放置在一起,所成的夹角为∠EAF=120°,设圆形工件分别与AE、AF相切于点B、C.小明想用刻度尺测量这个圆形工件的直径,但发现刻度尺的长度稍短些.请你设计两种不同的测量方法,仍用这把刻度尺并结合简单的计算,测出这个工件的直径.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com