
【题目】综合与探究
如图,在平面直角坐标系中,已知抛物线y=ax2+bx﹣8与x轴交于A,B两点,与y轴交于点C,直线l经过坐标原点O,与抛物线的一个交点为D,与抛物线的对称轴交于点E,连接CE,已知点A,D的坐标分别为(﹣2,0),(6,﹣8).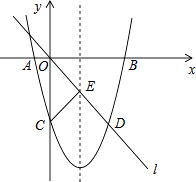
(1)求抛物线的函数表达式,并分别求出点B和点E的坐标;
(2)试探究抛物线上是否存在点F,使△FOE≌△FCE?若存在,请直接写出点F的坐标;若不存在,请说明理由;
(3)若点P是y轴负半轴上的一个动点,设其坐标为(0,m),直线PB与直线l交于点Q,试探究:当m为何值时,△OPQ是等腰三角形.
【答案】
(1)解:∵抛物线y=ax2+bx﹣8经过点A(﹣2,0),D(6,﹣8),
∴ ![]() ,解得
,解得 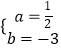 ,
,
∴抛物线解析式为y= ![]() x2﹣3x﹣8,
x2﹣3x﹣8,
∵y= ![]() x2﹣3x﹣8=
x2﹣3x﹣8= ![]() (x﹣3)2﹣
(x﹣3)2﹣ ![]() ,
,
∴抛物线对称轴为直线x=3,
又∵抛物线与x轴交于点A、B两点,点A坐标(﹣2,0),
∴点B坐标(8,0).
设直线l的解析式为y=kx,
∵经过点D(6,﹣8),
∴6k=﹣8,
∴k=﹣ ![]() ,
,
∴直线l的解析式为y=﹣ ![]() x,
x,
∵点E为直线l与抛物线的交点,
∴点E的横坐标为3,纵坐标为﹣ ![]() ×3=﹣4,
×3=﹣4,
∴点E坐标(3,﹣4)
(2)解:抛物线上存在点F使得△FOE≌△FCE,
此时点F纵坐标为﹣4,
∴ ![]() x2﹣3x﹣8=﹣4,
x2﹣3x﹣8=﹣4,
∴x2﹣6x﹣8=0,
x=3 ![]() ,
,
∴点F坐标(3+ ![]() ,﹣4)或(3﹣
,﹣4)或(3﹣ ![]() ,﹣4)
,﹣4)
(3)解:①如图1

中,当OP=OQ时,△OPQ是等腰三角形.
∵点E坐标(3,﹣4),
∴OE= ![]() =5,过点E作直线ME∥PB,交y轴于点M,交x轴于点H.则
=5,过点E作直线ME∥PB,交y轴于点M,交x轴于点H.则 ![]() =
= ![]() ,
,
∴OM=OE=5,
∴点M坐标(0,﹣5).
设直线ME的解析式为y=k1x﹣5,
∴3k1﹣5=﹣4,
∴k1= ![]() ,
,
∴直线ME解析式为y= ![]() x﹣5,
x﹣5,
令y=0,得 ![]() x﹣5=0,解得x=15,
x﹣5=0,解得x=15,
∴点H坐标(15,0),
∵MH∥PB,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴m=﹣ ![]() ,
,
②如图2 
中,当QO=QP时,△POQ是等腰三角形.
∵当x=0时,y= ![]() x2﹣3x﹣8=﹣8,
x2﹣3x﹣8=﹣8,
∴点C坐标(0,﹣8),
∴CE= ![]() =5,
=5,
∴OE=CE,
∴∠1=∠2,
∵QO=QP,
∴∠1=∠3,
∴∠2=∠3,
∴CE∥PB,
设直线CE交x轴于N,解析式为y=k2x﹣8,
∴3k2﹣8=﹣4,
∴k2= ![]() ,
,
∴直线CE解析式为y= ![]() x﹣8,
x﹣8,
令y=0,得 ![]() x﹣8=0,
x﹣8=0,
∴x=6,
∴点N坐标(6,0),
∵CN∥PB,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴m=﹣ ![]() .
.
③OP=PQ时,显然不可能,理由,
∵D(6,﹣8),
∴∠1<∠BOD,
∵∠OQP=∠BOQ+∠ABP,
∴∠PQO>∠1,
∴OP≠PQ,
综上所述,当m=﹣ ![]() 或﹣
或﹣ ![]() 时,△OPQ是等腰三角形
时,△OPQ是等腰三角形
【解析】(1)根据待定系数法求出抛物线解析式即可求出点B坐标,求出直线OD解析式即可解决点E坐标.(2)抛物线上存在点F使得△FOE≌△FCE,此时点F纵坐标为﹣4,令y=﹣4即可解决问题.(3))①如图1中,当OP=OQ时,△OPQ是等腰三角形,过点E作直线ME∥PB,交y轴于点M,交x轴于点H,求出点M、H的坐标即可解决问题.②如图2中,当QO=QP时,△POQ是等腰三角形,先证明CE∥PQ,根据平行线的性质列出方程即可解决问题.


科目:初中数学 来源: 题型:
【题目】如图,AB,CD是⊙O的两条互相垂直的直径,点O1 , O2 , O3 , O4分别是OA、OB、OC、OD的中点,若⊙O的半径为2,则阴影部分的面积为( ) 
A.8
B.4
C.4π+4
D.4π﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家商店要进行装修,若请甲、乙两个装修组同时施工,8天可以完成,需付两组费用共3520元;若先请甲组单独做6天,再请乙组单独做12天可完成,需付两组费用共3480元,问:
(1)甲、乙两组工作一天,商店应各付多少元?
(2)已知甲组单独做需12天完成,乙组单独做需24天完成,单独请哪组,商店所付费用最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知在数轴上有A、 B两点,点A表示的数是-6,点B表示的数是9.点P在数轴上从点A出发,以每秒2个单位的速度沿数轴正方向运动,同时,点Q在数轴上从点B出发,以每秒3个单位的速度沿数轴负方向运动,当点Q到达点A时,两点同时停止运动,设运动时间为t秒.
(1) AB=____ ;当t=1时,点Q表示的数是___ ;当t=___时,P、Q两点相遇;
(2)如图2,若点M为线段AP的中点,点N为线段BP中点,点P在运动过程中,线段MN的长度是否发生变化?若变化,请说明理由.若不变,请求出线段MN的长;
(3)如图3,若点M为线段的AP中点,点T为线段BQ中点,则点M表示的数为______;点T表示的数为______;MT=______ (用含t的代数式填空).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,点 D,E 分别在边 AC,AB 上,BD 与 CE 交于点 O,给出下列三个条件:①∠EBO=∠DCO;②BE=CD;③OB=OC.
(1)上述三个条件中,由哪两个条件可以判定△ABC 是等腰三角形?(用序号写出所有成立的情形)
(2)请选择(1)中的一种情形,写出证明过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班在一次班会课上,就“遇见路人摔倒后如何处理”的主题进行讨论,并对全班 50 名学生的处理方式进行统计,得出相关统计表和统计图.
组别 | A | B | C | D |
处理方式 | 迅速离开 | 马上救助 | 视情况而定 | 只看热闹 |
人数 | m | 30 | n | 5 |
请根据表图所提供的信息回答下列问题:
(1)统计表中的 m= ,n= ;
(2)补全频数分布直方图;
(3)若该校有 2000 名学生,请据此估计该校学生采取“马上救助”方式的学生有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=2,BF=8,BC=AE=6,CE=CF=7,则△CDF与四边形ABDE的面积比值是( )
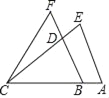
A. 1:1 B. 2:1 C. 1:2 D. 2:3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y=![]() 的图象经过点(﹣1,-2
的图象经过点(﹣1,-2![]() ),点A是该图象第一象限分支上的动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角三角形ABC,顶点C在第四象限,AC与x轴交于点D,当
),点A是该图象第一象限分支上的动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角三角形ABC,顶点C在第四象限,AC与x轴交于点D,当![]() =
=![]() 时,则点C的坐标为 .
时,则点C的坐标为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,现有以下三个条件:①AB∥CD,②∠B=∠C,③∠E=∠F.请你以其中两个作为题设,另一个作为结论构造命题.(1)你构造的是哪几个命题?(2)你构造的命题是真命题还是假命题?若是真命题,请给予证明;若是假命题,请举出反例.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com