
探索归纳:
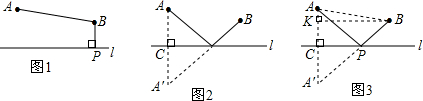
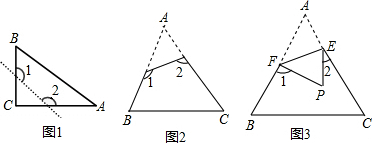
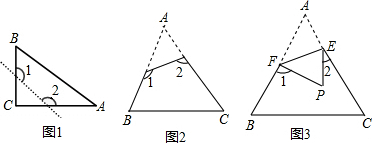
(1)如图1,已知△ABC为直角三角形,∠A=90°,若沿图中虚线剪去∠A,则∠1+∠2等于 ( )
A. 90° B. 135° C. 270° D. 315°
(2)如图2,已知△ABC中,∠A=40°,剪去∠A后成四边形,则∠1+∠2=_______

(3)如图2,根据(1)与(2)的求解过程,请你归纳猜想∠1+∠2与∠A的关系是________________
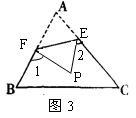
(4)如图3,若没有剪掉,而是把它折成如图3形状,试探究∠1+∠2与∠A的关系并说明理由.
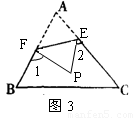
(1)∵四边形的内角和为360°,直角三角形中两个锐角和为90°
∴∠1+∠2=360°-(∠A+∠B)=360°-90°=270°.
∴∠1+∠2等于270°.C;
(2)∠1+∠2=180°+40°=220°.220°;
(3)∠1+∠2=180°+∠A;
(4)方法一:∵△EFP是由△EFA折叠得到的
∴∠AFE=∠PFE,∠AEF=∠PEF
∴∠1=180°-2∠AFE,∠2=180°-2∠AEF
∴∠1+∠2=360°-2(∠AFE+∠AEF)
又∵∠AFE+∠AEF=180°-∠A
∴∠1+∠2=360°-2(180°-∠A)=2∠A
方法二: ∵∠1+∠PFE=∠AEF+∠A, ∠2+∠PEF=∠AFE+∠A
∴∠1+∠PFE+∠2+∠PEF=∠AEF+∠AFE+2∠A
∵△EFP是由△EFA折叠得到的
∴∠AFE=∠PFE,∠AEF=∠PEF
∴∠1+∠2=2∠A
【解析】(1) 本题利用了四边形内角和为360°和直角三角形的性质求解;
(2) 根据三角形的外角等于与它不相邻的两个内角和求解;
(3)根据(1)、(2)归纳出结论;
(4) 折问题要在图形是找着相等的量.图1中DE为折痕,有∠A=∠DA′A,再利用外角的性质可得结论∠BDA′=2∠A图2中∠A与∠DA′E是相等的,再结合四边形的内角和及互补角的性质可得结论∠BDA′+∠CEA′=2∠A图3中由于折叠∠A与∠DA′E是相等的,再两次运用三角形外角的性质可得结论.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2011-2012学年福建邵武市邵中片七年级下学期期中测试数学试卷(带解析) 题型:解答题
探索归纳:
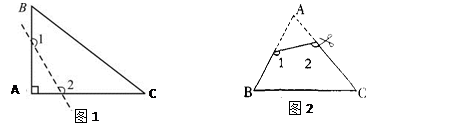
(1)如图1,已知△ABC为直角三角形,∠A=90°,若沿图中虚线剪去∠A,则∠1+∠2等于 ( )
| A.90° | B.135° | C.270° | D.315° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com