
【题目】如图所示,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下四个结论:①△ACD≌△BCE;②AD=BE;③∠AOB=60°;④△CPQ是等边三角形.其中正确的是( )

A. ①②③④B. ②③④C. ①③④D. ①②③
【答案】A
【解析】
由已知条件运用等边三角形的性质得到三角形全等,进而得到更多结论,然后运用排除法,对各个结论进行验证从而确定最后的答案.
∵△ABC和△CDE是正三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∵∠ACD=∠ACB+∠BCD,∠BCE=∠DCE+∠BCD,
∴∠ACD=∠BCE,
∴△ADC≌△BEC(SAS),故①正确,
∴AD=BE,故②正确;
∵△ADC≌△BEC,
∴∠ADC=∠BEC,
∴∠AOB=∠DAE+∠AEO=∠DAE+∠ADC=∠DCE=60°,故③正确;
∵CD=CE,∠DCP=∠ECQ=60°,∠ADC=∠BEC,
∴△CDP≌△CEQ(ASA).
∴CP=CQ,
∴∠CPQ=∠CQP=60°,
∴△CPQ是等边三角形,故④正确;
故选:A.


科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,若动点
,若动点![]() 从点
从点![]() 开始,按
开始,按![]() 的路径
的路径![]() 运动一周,且速度为每秒
运动一周,且速度为每秒![]() ,设运动的时间为
,设运动的时间为![]() 秒.
秒.
(![]() )求
)求![]() 为何值时,
为何值时,![]() 把
把![]() 的周长分成相等的两部分
的周长分成相等的两部分
(![]() )求
)求![]() 为何值时,
为何值时,![]() 把
把![]() 的面积分成相等的两部分;并求此时
的面积分成相等的两部分;并求此时![]() 的长.
的长.
(![]() )求
)求![]() 为何值时,
为何值时,![]() 为等腰三角形?(请直接写出答案)
为等腰三角形?(请直接写出答案)


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.

(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,∠A=30°.

(1)用尺规作图作AB边上的中垂线DE,交AC于点D,交AB于点E.(保留作图痕迹,不要求写作法和证明);
(2)连接BD,求证:BD平分∠CBA.
查看答案和解析>>
科目:初中数学 来源: 题型:
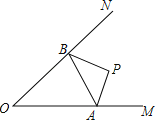
【题目】如图,已知∠MON=40°,P为∠MON内一定点,OM上有一点A,ON上有一点B,当△PAB的周长取最小值时,∠APB的度数是_____°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)(学习心得)
小刚同学在学习完“圆”这一章内容后,感觉到一些几何问题,如果添加辅助圆,运用圆的知识解决,可以使问题变得非常容易.
例如:如图1,在△ABC中,AB=AC,∠BAC=90°,D是△ABC外一点,且AD=AC,求∠BDC的度数,若以点A为圆心,AB为半径作辅助圆⊙A,则点C、D必在⊙A上,∠BAC是⊙A的圆心角,而∠BDC是圆周角,从而可容易得到∠BDC= °.
(2)(问题解决)
如图2,在四边形ABCD中,∠BAD=∠BCD=90°,∠BDC=25°,求∠BAC的度数.
小刚同学认为用添加辅助圆的方法,可以使问题快速解决,他是这样思考的:△ABD的外接圆就是以BD的中点为圆心,![]() BD长为半径的圆;△ACD的外接圆也是以BD的中点为圆心,
BD长为半径的圆;△ACD的外接圆也是以BD的中点为圆心,![]() BD长为半径的圆.这样A、B、C、D四点在同一个圆上,进而可以利用圆周角的性质求出∠BAC的度数,请运用小刚的思路解决这个问题.
BD长为半径的圆.这样A、B、C、D四点在同一个圆上,进而可以利用圆周角的性质求出∠BAC的度数,请运用小刚的思路解决这个问题.
(3)(问题拓展)
如图3,在△ABC中,∠BAC=45°,AD是BC边上的高,且BD=4,CD=2,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AB=2,AC=![]() ,AD是△ABC的高,且 BD=1.
,AD是△ABC的高,且 BD=1.
(1)求 BC的长.
(2)E是边AC上的一点,作射线BE,分别过点A、C 作 AF⊥BE于点 F,CG⊥BE于点 G,如图2,若 BE=![]() ,求 AF与 CG的和.
,求 AF与 CG的和.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com