
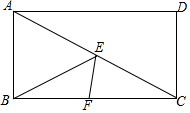
 如图,在矩形ABCD中,AB=2,BC=4,点E和点F分别是AC和BC上的动点,在点E和点F运动的过程中,BE+EF的最小值为( )
如图,在矩形ABCD中,AB=2,BC=4,点E和点F分别是AC和BC上的动点,在点E和点F运动的过程中,BE+EF的最小值为( )| A. | $\frac{16}{5}$ | B. | $\frac{8}{5}$ | C. | $\frac{8\sqrt{5}}{5}$ | D. | $\frac{2\sqrt{5}}{5}$ |
分析 作点B关于AC的对称点B′,过点B′作B′F⊥BC于F,交AC于E,连接CB′交AD于P,连接BE,再根据矩形、轴对称、等腰三角形的性质得出PA=PC,那么在Rt△CDP中,运用勾股定理求出PC的长,然后由cos∠B′CF=cos∠CPD,求出CF的长.
解答 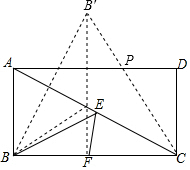 解:如图,作点B关于AC的对称点B′,过点B′作B′F⊥BC于F,交AC于E,连接CB′交AD于P,连接BE,
解:如图,作点B关于AC的对称点B′,过点B′作B′F⊥BC于F,交AC于E,连接CB′交AD于P,连接BE,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠BCA=∠PAC,
∵点B关于AC的对称点是B′,
∴∠PCA=∠BCA,
∴∠PAC=∠PCA,
∴PA=PC.
令PA=x,则PC=x,PD=4-x.
在Rt△CDP中,∵PC2=PD2+CD2,
∴x2=(4-x)2+22,
∴x=2.5,
∵cos∠B′CF=cos∠CPD,
∴CF:B′C=DP:CP,
∴CF:4=1.5:2.5,
∴CF=$\frac{12}{5}$,
∴B′F=$\sqrt{B′{C}^{2}-C{F}^{2}}$=$\frac{16}{5}$,
∴BE+EF的最小值为=$\frac{16}{5}$.
故选:A.
点评 本题主要考查了轴对称-最短路线问题,矩形的性质,根据垂线段最短作出辅助线,确定点E,F的位置是解答此题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点.
如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
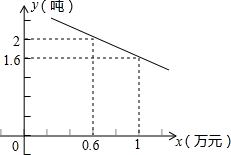 伴随经济发展和生活水平的日益提高,水果超市如雨后春笋般兴起.万松园一水果超市从外地购进一批水果,其进货成本是每吨0.4万元,根据预测,此批水果一段时间内的销量y(吨)(纵坐标)与每吨的销售价x万元(横坐标)之间的函数关系如图所示.
伴随经济发展和生活水平的日益提高,水果超市如雨后春笋般兴起.万松园一水果超市从外地购进一批水果,其进货成本是每吨0.4万元,根据预测,此批水果一段时间内的销量y(吨)(纵坐标)与每吨的销售价x万元(横坐标)之间的函数关系如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com