
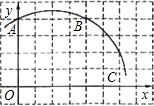
 如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:
如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:分析 (1)找到AB,BC的垂直平分线的交点即为圆心坐标;
(2)利用勾股定理可求得圆的半径;易得△AOD≌△DEC,那么∠OAD=∠CDE,即可得到圆心角的度数为90°,根据弧长公式可得;
(3)求出DE的长与半径比较可得.
解答 解:(1)如图,D点坐标为(2,0),
故答案为:(2,0);
(2)AD=$\sqrt{A{O}^{2}+O{D}^{2}}$=2$\sqrt{5}$;
作CE⊥x轴,垂足为E.
∵△AOD≌△DEC,
∴∠OAD=∠CDE,
又∵∠OAD+∠ADO=90°,
∴∠CDE+∠ADO=90°,
∴扇形DAC的圆心角为90度,
∴$\widehat{AC}$的长为$\frac{90•π•2\sqrt{5}}{180}$=$\sqrt{5}$π;
(3)点E到圆心D的距离为4$<2\sqrt{5}$,
∴点E在⊙D内部.
点评 本题主要考查点与圆的位置关系、垂径定理、弧长公式等,用到的知识点为:非直径的弦的垂直平分线经过圆心.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
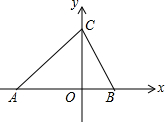 如图,在平面直角坐标系中,A(-4,0),B(2,0),点C在y轴正半轴上,且S△ABC=18.
如图,在平面直角坐标系中,A(-4,0),B(2,0),点C在y轴正半轴上,且S△ABC=18.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 年龄x | 生存人数l | 死亡人数d |
| 0 | 1000000 | 661 |
| 1 | 999339 | 536 |
| 30 | 991476 | 403 |
| 31 | 991074 | 428 |
| 61 | 938005 | 6064 |
| 62 | 931941 | 6743 |
| 63 | 925198 | 7489 |
| 64 | 917709 | 8314 |
| 79 | 649175 | 32429 |
| 80 | 616746 | 34398 |
| 81 | 582347 | 36253 |
| 82 | 546095 | 37950 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com