
【题目】“城市发展 交通先行”,成都市今年在中心城区启动了缓堵保畅的二环路高架桥快速通道建设工程,建成后将大大提升二环路的通行能力.研究表明,某种情况下,高架桥上的车流速度V(单位:千米/时)是车流密度x(单位:辆/千米)的函数,且当0<x≤28时,V=80;当28<x≤188时,V是x的一次函数.函数关系如图所示. 
(1)求当28<x≤188时,V关于x的函数表达式;
(2)若车流速度V不低于50千米/时,求当车流密度x为多少时,车流量P(单位:辆/时)达到最大,并求出这一最大值. (注:车流量是单位时间内通过观测点的车辆数,计算公式为:车流量=车流速度×车流密度)
【答案】
(1)解:设函数解析式为V=kx+b,
则 ![]() ,
,
解得: 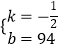 ,
,
故V关于x的函数表达式为:V=﹣ ![]() x+94(28<x≤188)
x+94(28<x≤188)
(2)解:当V≥50时,包含V=80,由函数图象可知,
当V=80时,0<x≤28,此时P=80x,P是x的增函数,
当x=28时,P最大=2240,
由题意得,V=﹣ ![]() x+94≥50,
x+94≥50,
解得:x≤88,
又P=Vx=(﹣ ![]() x+94)x=﹣
x+94)x=﹣ ![]() x2+94x,
x2+94x,
当28<x≤88时,函数为增函数,即当x=88时,P取得最大值,
故Pmax=﹣ ![]() ×882+94×88=4400,
×882+94×88=4400,
∵2240<4400,
所以,当x=88时,P取得最大为4400,
答:当车流密度达到88辆/千米时,车流量P达到最大,最大值为4400辆/时
【解析】(1)设函数解析式为y=kx+b,将点(28,80),(188,0)代入即可得出答案.(2)先有车流速度V不低于50千米/时得出x的范围,然后求出P的表达式,继而根据二次函数的最值求解方法可得出答案.


科目:初中数学 来源: 题型:
【题目】某商厦进货员在苏州发现了一种应季围巾,用8000元购进一批围巾后,发现市场还有较大的需求,又在上海用17600元购进了同一种围巾,数量恰好是在苏州所购数量的2倍,但每条比在苏州购进的多了4元.问某商厦在苏州、上海分别购买了多少条围巾?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某饮料厂以300千克的A种果汁和240千克的B种果汁为原料,配制生产甲、乙两种新型饮料,已知每千克甲种饮料含0.6千克A种果汁,含0.3千克B种果汁;每千克乙种饮料含0.2千克A种果汁,含0.4千克B种果汁.饮料厂计划生产甲、乙两种新型饮料共650千克,设该厂生产甲种饮料x(千克).
(1)列出满足题意的关于x的不等式组,并求出x的取值范围;
(2)已知该饮料厂的甲种饮料销售价是每1千克3元,乙种饮料销售价是每1千克4元,那么该饮料厂生产甲、乙两种饮料各多少千克,才能使得这批饮料销售总金额最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.相等的角是对顶角
B.在同一平面内,不平行的两条直线一定互相垂直
C.点P(2,﹣3)在第四象限
D.一个数的算术平方根一定是正数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段AB。
![]()
(1)用尺规作图的方法作出线段AB的垂直平分线l(保留作图痕迹,不要求写出作法);
(2)在(1)中所作的直线l上任意取两点M、N(线段AB的上方),连接AM、AN。BM、BN。
求证:∠MAN=∠MBN。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个大小一样的直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到![]() 的位置,AB=12cm,DH=4cm,平移的距离是8cm,则阴影面积是________.
的位置,AB=12cm,DH=4cm,平移的距离是8cm,则阴影面积是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,对于P(x,y)作变换得到P′(﹣y+1,x+1),例如:A1(3,1)作上述变换得到A2(0,4),再将A2做上述变换得到A3___________,这样依次得到A1,A2,A3,…An;…,则A2018的坐标为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
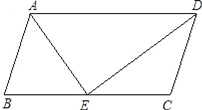
【题目】如图,已知平行四边形ABCD,DE是∠ADC的角平分线,交BC于点E.
(1)求证:CD=CE;
(2)若BE=CE,∠B=80°,求∠DAE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用1─9中的三个数字,如2、3、5组成数字不重复的三位整数,共有6个,计算方法为:3×2×1=6,现有1个老师和4个学生站成一排照相,老师站在正中间的不同站法有______种?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com