
【题目】如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CAB=2∠CBF.
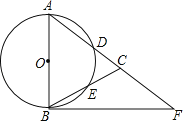
(1)试判断直线BF与⊙O的位置关系,并说明理由;
(2)若AB=6,BF=8,求tan∠CBF.
【答案】(1)BF为⊙O的切线;理由详见解析;(2)![]() .
.
【解析】
试题分析:(1)连接AE.通过AB⊥BF,点B在⊙O上可以推知BF为⊙O的切线;
(2)作辅助线CG(过点C作CG⊥BF于点G)构建平行线AB∥CG.由“平行线截线段成比例”知![]() =
=![]() =
=![]() ,从而求得FG的值;然后根据图形中相关线段间的和差关系求得直角三角形CBG的两直角边BG、CG的长度;最后由锐角三角函数的定义来求tan∠CBF的值.
,从而求得FG的值;然后根据图形中相关线段间的和差关系求得直角三角形CBG的两直角边BG、CG的长度;最后由锐角三角函数的定义来求tan∠CBF的值.
试题解析:(1)BF为⊙O的切线.理由如下:
连接AE.
∵AB为⊙O的直径,
∴∠AEB=90°(直径所对的圆周角是直角),
∴∠BAE+∠ABE=90°(直角三角形的两个锐角互余);
又∵AB=AC,AE⊥BC,
∴AE平分∠BAC,即∠BAE=∠CAE;
∵∠CAB=2∠CBF,
∴∠BAE=∠CBF,
∴∠BAE+∠ABE=∠ABE+∠CBF=90°,即AB⊥BF,
∵OB是半径,
∴BF为⊙O的切线;
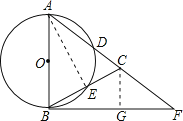
(2)过点C作CG⊥BF于点G.
在Rt△ABF中,AB=6,BF=8,
∴AF=10(勾股定理);
又∵AC=AB=6
∴CF=4;
∵CG⊥BF,AB⊥BF,
∴CG∥AB,
∴![]() =
=![]() =
=![]() ,(平行线截线段成比例),
,(平行线截线段成比例),
∴FG=![]() ,
,
由勾股定理得:CG=![]() =
=![]() ,
,
∴BG=BF﹣FG=8﹣![]() =
=![]() ,
,
在Rt△BCG中,tan∠CBF=![]() =
=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
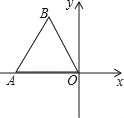
【题目】如图,点O为平面直角坐标系的原点,点A在x轴上,△OAB是边长为4的等边三角形,以O为旋转中心,将△OAB按顺时针方向旋转60°,得到△OA′B′,那么点A′的坐标为( )
A. (2,2![]() ) B. (﹣2,4) C. (﹣2,2
) B. (﹣2,4) C. (﹣2,2![]() ) D. (﹣2,2
) D. (﹣2,2![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于数轴上的![]() 三点,给出如下定义:若其中一个点与其他两个点的距离恰好满足2倍的数量关系,则称该点是其他两点的“倍联点”. 例如数轴上点
三点,给出如下定义:若其中一个点与其他两个点的距离恰好满足2倍的数量关系,则称该点是其他两点的“倍联点”. 例如数轴上点![]() 所表示的数分别为1,3,4,满足
所表示的数分别为1,3,4,满足![]() ,此时点
,此时点![]() 是点
是点![]() 的“倍联点”.
的“倍联点”.
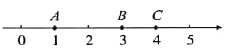
若数轴上点![]() 表示
表示![]() ,点
,点![]() 表示6,回答下列问题:
表示6,回答下列问题:
(1)数轴上点![]() 分別对应0,3. 5和11,则点_________是点
分別对应0,3. 5和11,则点_________是点![]() 的“倍联点”,点
的“倍联点”,点![]() 是________这两点的“倍联点”;
是________这两点的“倍联点”;
(2)已知动点![]() 在点
在点![]() 的右侧,若点
的右侧,若点![]() 是点
是点![]() 的倍联点,求此时点
的倍联点,求此时点![]() 表示的数.
表示的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某检修小组从![]() 地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶纪录如下.(单位:
地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶纪录如下.(单位:![]() )
)
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
|
|
|
|
|
|
|
(1)在第__________次记录时距![]() 地最远;
地最远;
(2)求收工时距![]() 地多远?
地多远?
(3)若每千米耗油![]() 升,每升汽油需
升,每升汽油需![]() 元,问检修小组工作一天需汽油费多少元?
元,问检修小组工作一天需汽油费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(10.0)及在第一象限的动点P(x,y),且x+y=12,设△OPA的面积为S。
(1)求S关于x的函数解析式;
(2)求x的取值范围;
(3)当S=15时,求P点坐标;
查看答案和解析>>
科目:初中数学 来源: 题型:
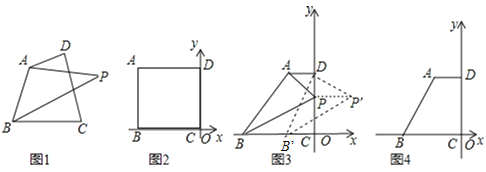
【题目】如图1,点P为四边形ABCD所在平面上的点,如果∠PAD=∠PBC,则称点P为四边形ABCD关于A、B的等角点,以点C为坐标原点,BC所在直线为![]() 轴建立平面直角坐标系,点B的横坐标为﹣6.
轴建立平面直角坐标系,点B的横坐标为﹣6.
(1)如图2,若A、D两点的坐标分别为A(﹣6,4)、D(0,4),点P在DC边上,且点P为四边形ABCD关于A、B的等角点,则点P的坐标为 _________ ;
(2)如图3,若A、D两点的坐标分别为A(﹣2,4)、D(0,4).
①若P在DC边上时,则四边形ABCD关于A、B的等角点P的坐标为 _________ ;
②在①的条件下,将PB沿![]() 轴向右平移
轴向右平移![]() 个单位长度(0<
个单位长度(0<![]() <6)得到线段P′B′,连接P′D,B′D,试用含
<6)得到线段P′B′,连接P′D,B′D,试用含![]() 的式子表示P′D2+B′D2,并求出使P′D2+B′D2取得最小值时点P′的坐标;
的式子表示P′D2+B′D2,并求出使P′D2+B′D2取得最小值时点P′的坐标;
③如图4,若点P为四边形ABCD关于A、B的等角点,且点P坐标为(1, ![]() ),求
),求![]() 的值;
的值;
④以四边形ABCD的一边为边画四边形,所画的四边形与四边形ABCD有公共部分,若在所画的四边形内存在一点P,使点P分别是各相邻两顶点的等角点,且四对等角都相等,请直接写出所有满足条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】河南开封的西瓜个大瓤红且甜,全国知名![]() 某瓜农准备从某货运公司租用大小两种型号的货车运输西瓜到外地销售,已知一辆大型货车和一辆小型货车每次共运10吨;两辆大型货车和三辆小型渣货车每次共运24吨.
某瓜农准备从某货运公司租用大小两种型号的货车运输西瓜到外地销售,已知一辆大型货车和一辆小型货车每次共运10吨;两辆大型货车和三辆小型渣货车每次共运24吨.
![]() 求一辆大型货车和一辆小型货车每次各运西瓜多少吨?
求一辆大型货车和一辆小型货车每次各运西瓜多少吨?
![]() 已知一辆大型货车运输花费为400元
已知一辆大型货车运输花费为400元![]() 次,一辆小型货车运输花费为300元
次,一辆小型货车运输花费为300元![]() 次,计划用20辆货车运输,且每次运输西瓜总重量不少于96吨,如何安排才能使每次运费最低,最低费用是多少?
次,计划用20辆货车运输,且每次运输西瓜总重量不少于96吨,如何安排才能使每次运费最低,最低费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() ,
,![]() ,
,![]() ,设
,设![]() ,
,![]() ,
,![]() ,……,
,……,![]()
(1)计算![]() ___________,
___________,![]() ____________,
____________,![]() ____________
____________
(2)写出![]() ,
,![]() ,
,![]() ,
,![]() 四者之间的关系,并证明你的结论.
四者之间的关系,并证明你的结论.
(3)根据(2)的结论,直接写出![]() 的值是_____________
的值是_____________
查看答案和解析>>
科目:初中数学 来源: 题型:
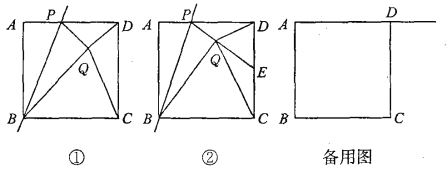
【题目】如图①,已知正方形ABCD的边长为1,点P是AD边上的一个动点,点A关于直线BP的对称点是点Q,连接PQ、DQ、CQ、BQ,设AP=x.
(1)BQ+DQ的最小值是_______,此时x的值是_______;
(2)如图②,若PQ的延长线交CD边于点E,并且∠CQD=90°.
①求证:点E是CD的中点; ②求x的值.
(3)若点P是射线AD上的一个动点,请直接写出当△CDQ为等腰三角形时x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com