
【题目】如图,在 ABCD中,CD=2AD,BE⊥AD于点E,F为DC的中点,连结EF、BF,下列结论:①∠ABC=2∠ABF;②EF=BF;③S四边形DEBC=2S△EFB;④∠CFE=3∠DEF,其中正确结论的个数共有( ).

A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【解析】
如图延长EF交BC的延长线于G,取AB的中点H连接FH.证明△DFE≌△FCG 得EF=FG,BE⊥BG,四边形BCFH是菱形即可解决问题;
如图延长EF交BC的延长线于G,取AB的中点H连接FH.
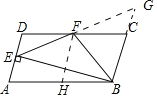
∵CD=2AD,DF=FC,
∴CF=CB,
∴∠CFB=∠CBF,
∵CD∥AB,
∴∠CFB=∠FBH,
∴∠CBF=∠FBH,
∴∠ABC=2∠ABF.故①正确,
∵DE∥CG,
∴∠D=∠FCG,
∵DF=FC,∠DFE=∠CFG,
∴△DFE≌△FCG,
∴FE=FG,
∵BE⊥AD,
∴∠AEB=90°,
∵AD∥BC,
∴∠AEB=∠EBG=90°,
∴BF=EF=FG,故②正确,
∵S△DFE=S△CFG,
∴S四边形DEBC=S△EBG=2S△BEF,故③正确,
∵AH=HB,DF=CF,AB=CD,
∴CF=BH,∵CF∥BH,
∴四边形BCFH是平行四边形,
∵CF=BC,
∴四边形BCFH是菱形,
∴∠BFC=∠BFH,
∵FE=FB,FH∥AD,BE⊥AD,
∴FH⊥BE,
∴∠BFH=∠EFH=∠DEF,
∴∠EFC=3∠DEF,故④正确,
故选:D.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】如图1,点M为直线AB上一动点, ![]() 都是等边三角形,连接BN
都是等边三角形,连接BN
![]() 求证:
求证: ![]() ;
;
![]() 分别写出点M在如图2和图3所示位置时,线段AB、BM、BN三者之间的数量关系
分别写出点M在如图2和图3所示位置时,线段AB、BM、BN三者之间的数量关系![]() 不需证明
不需证明![]() ;
;
![]() 如图4,当
如图4,当![]() 时,证明:
时,证明: ![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c交x轴于点A(﹣3,0)和点B,交y轴于点C(0,3).
(1)求抛物线的函数表达式;
(2)若点P在抛物线上,且S△AOP=4SBOC , 求点P的坐标;
(3)如图b,设点Q是线段AC上的一动点,作DQ⊥x轴,交抛物线于点D,求线段DQ长度的最大值.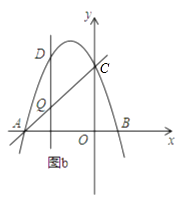
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,对于点
中,对于点![]() ,我们把点
,我们把点![]() 叫做点
叫做点![]() 的衍生点.已知点
的衍生点.已知点![]() 的衍生点为
的衍生点为![]() ,点
,点![]() 的衍生点为
的衍生点为![]() ,点
,点![]() 的衍生点为
的衍生点为![]() 这样依次得到点
这样依次得到点![]() 若点
若点![]() 的坐标为
的坐标为![]() ,若点
,若点![]() 在第四象限,则
在第四象限,则![]() 范围分别为______________.
范围分别为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,对角线AC , BD相交于点O , 且AC=6cm,BD=8cm,动点P , Q分别从点B , D同时出发,运动速度均为1cm/s,点P沿B→C→D运动,到点D停止,点Q沿D→O→B运动,到点O停止1s后继续运动,到点B停止,连接AP , AQ , PQ . 设△APQ的面积为y(cm2)(这里规定:线段是面积0的几何图形),点P的运动时间为x(s). 
(1)填空:AB=cm,AB与CD之间的距离为cm;
(2)当4≤x≤10时,求y与x之间的函数解析式;
(3)直接写出在整个运动过程中,使PQ与菱形ABCD一边平行的所有x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在锐角△ABC中,∠ABC=60°,BC=2cm,BD平分∠ABC交AC于点D,点M,N分别是BD和BC边上的动点,则MN+MC的最小值是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若BC=EC,∠BCE=∠ACD,则添加不能使△ABC≌△DBC的条件是( )

A.AB=DE B.∠B=∠E C.AC=DC D.∠A=∠D
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com