
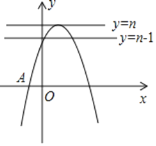
【题目】已知抛物线y=ax2+bx+c(a<0)与x轴交于点A(﹣1,0),与y轴的交点在(0,2),(0,3)之间(包含端点),顶点坐标为(1,n),则下列结论:
①4a+2b<0;
②﹣1≤a≤![]() ;
;
③对于任意实数m,a+b≥am2+bm总成立;
④关于x的方程ax2+bx+c=n﹣1有两个不相等的实数根.
其中结论正确的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】
①由抛物线的顶点横坐标可得出b=-2a,进而可得出4a+2b=0,结论①错误;
②利用一次函数图象上点的坐标特征结合b=-2a可得出a=-![]() ,再结合抛物线与y轴交点的位置即可得出-1≤a≤-
,再结合抛物线与y轴交点的位置即可得出-1≤a≤-![]() ,结论②正确;
,结论②正确;
③由抛物线的顶点坐标及a<0,可得出n=a+b+c,且n≥ax2+bx+c,进而可得出对于任意实数m,a+b≥am2+bm总成立,结论③正确;
④由抛物线的顶点坐标可得出抛物线y=ax2+bx+c与直线y=n只有一个交点,将直线下移可得出抛物线y=ax2+bx+c与直线y=n-1有两个交点,进而可得出关于x的方程ax2+bx+c=n-1有两个不相等的实数根,结合④正确.
:①∵抛物线y=ax2+bx+c的顶点坐标为(1,n),
∴-![]() =1,
=1,
∴b=-2a,
∴4a+2b=0,结论①错误;
②∵抛物线y=ax2+bx+c与x轴交于点A(-1,0),
∴a-b+c=3a+c=0,
∴a=-![]() .
.
又∵抛物线y=ax2+bx+c与y轴的交点在(0,2),(0,3)之间(包含端点),
∴2≤c≤3,
∴-1≤a≤-![]() ,结论②正确;
,结论②正确;
③∵a<0,顶点坐标为(1,n),
∴n=a+b+c,且n≥ax2+bx+c,
∴对于任意实数m,a+b≥am2+bm总成立,结论③正确;
④∵抛物线y=ax2+bx+c的顶点坐标为(1,n),
∴抛物线y=ax2+bx+c与直线y=n只有一个交点,
又∵a<0,
∴抛物线开口向下,
∴抛物线y=ax2+bx+c与直线y=n-1有两个交点,
∴关于x的方程ax2+bx+c=n-1有两个不相等的实数根,结合④正确.
故选:C.


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠A=∠B=90°,P是线段AB上的一个动点.
(1)若AD=2,BC=6,AB=8,且以A,D,P为顶点的三角形与以B,C,P为顶点的三角形相似,求AP的长;
(2)若AD=a,BC=b,AB=m,则当a,b,m满足什么关系时,一定存在点P使△ADP∽△BPC?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,∠AOB=90°,∠OAB=30°,反比例函数y1=![]() 的图象经过点A,反比例函数y2=
的图象经过点A,反比例函数y2=![]() 的图象经过点B,则下列关于m,n的关系正确的是( )
的图象经过点B,则下列关于m,n的关系正确的是( )

A. m=-3n B. m=-![]() n C. m=-
n C. m=-![]() n D. m=
n D. m=![]() n
n
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:有一堵长为![]() 的墙,利用这堵墙和长为
的墙,利用这堵墙和长为![]() 的篱笆围成一个矩形养鸡场,怎样围面积最大?最大面积是多少?
的篱笆围成一个矩形养鸡场,怎样围面积最大?最大面积是多少?
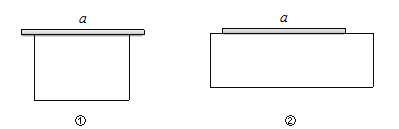
题意理解:根据题意,有两种设计方案:一边靠墙(如图①)和一边“包含”墙(如图②).
特例分析:
(1)当![]() 时,若按图①的方案设计,则该方案中养鸡场的最大面积是
时,若按图①的方案设计,则该方案中养鸡场的最大面积是 ![]() ;若按图②的方案设计,则该方案中养鸡场的最大面积是
;若按图②的方案设计,则该方案中养鸡场的最大面积是 ![]() .
.
(2)当![]() 时,解决“问题情境”中的问题.
时,解决“问题情境”中的问题.
解决问题:(3)直接写出“问题情境”中的问题的答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
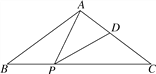
【题目】如图,在△ABC中,AB=AC,点P、D分别是BC、AC边上的点,且∠APD=∠B.
(1)求证:AC·CD=CP·BP;
(2)若AB=10,BC=12,当PD∥AB时,求BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件50元.当售价为每件70元时,每星期可卖出300件,现需降价处理,且经市场调查:每降价1元,每星期可多卖出20件.在确保盈利的前提下,解答下列问题:
(1)若设每件降价x元、每星期售出商品的利润为y元,请写出y与x的函数关系式,并求出自变量x的取值范围;
(2)当降价多少元时,每星期的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 某工厂质检员检测某批灯泡的使用寿命采用普查法
B. 已知一组数据1,a,4,4,9,它的平均数是4,则这组数据的方差是7.6
C. 12名同学中有两人的出生月份相同是必然事件
D. 在“等边三角形、正方形、等腰梯形、矩形、正六边形、正五边形”中,任取其中一个图形,恰好既是中心对称图形,又是轴对称图形的概率是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,其中正确的命题个数有( )
(1)在△ABC中,已知AB=6,AC=2![]() ,∠B=45°,则∠C的度数为60°;
,∠B=45°,则∠C的度数为60°;
(2)已知⊙O的半径为5,圆心O到弦AB的距离为3,则⊙O上到弦AB所在直线的距离为2的点有3个;
(3)圆心角是180°的扇形是一个半圆;
(4)已知点P是线段AB的黄金分割点,若AB=1,则AP=![]() .
.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com