
【题目】(3分)如图,在等边△ABC中,AB=10,BD=4,BE=2,点P从点E出发沿EA方向运动,连接PD,以PD为边,在PD右侧按如图方式作等边△DPF,当点P从点E运动到点A时,点F运动的路径长是( )
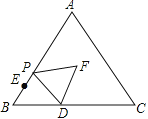
A. 8 B. 10 C. 3π D. 5π
【答案】A
【解析】试题连结DE,作FH⊥BC于H,如图,∵△ABC为等边三角形,∴∠B=60°,过D点作DE′⊥AB,则BE′=![]() BD=2,∴点E′与点E重合,∴∠BDE=30°,DE=
BD=2,∴点E′与点E重合,∴∠BDE=30°,DE=![]() BE=
BE=![]() ,∵△DPF为等边三角形,∴∠PDF=60°,DP=DF,∴∠EDP+∠HDF=90°,∵∠HDF+∠DFH=90°,∴∠EDP=∠DFH,在△DPE和△FDH中,∵∠PED=∠DHF,∠EDP=∠DFH,DP=FD,∴△DPE≌△FDH,∴FH=DE=
,∵△DPF为等边三角形,∴∠PDF=60°,DP=DF,∴∠EDP+∠HDF=90°,∵∠HDF+∠DFH=90°,∴∠EDP=∠DFH,在△DPE和△FDH中,∵∠PED=∠DHF,∠EDP=∠DFH,DP=FD,∴△DPE≌△FDH,∴FH=DE=![]() ,∴点P从点E运动到点A时,点F运动的路径为一条线段,此线段到BC的距离为
,∴点P从点E运动到点A时,点F运动的路径为一条线段,此线段到BC的距离为![]() ,当点P在E点时,作等边三角形DEF1,∠BDF1=30°+60°=90°,则DF1⊥BC,当点P在A点时,作等边三角形DAF2,作F2Q⊥BC于Q,则△DF2Q≌△ADE,所以DQ=AE=10﹣2=8,∴F1F2=DQ=8,∴当点P从点E运动到点A时,点F运动的路径长为8.故选A.
,当点P在E点时,作等边三角形DEF1,∠BDF1=30°+60°=90°,则DF1⊥BC,当点P在A点时,作等边三角形DAF2,作F2Q⊥BC于Q,则△DF2Q≌△ADE,所以DQ=AE=10﹣2=8,∴F1F2=DQ=8,∴当点P从点E运动到点A时,点F运动的路径长为8.故选A.



科目:初中数学 来源: 题型:
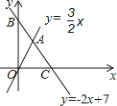
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别相交于点C、B,与直线
轴分别相交于点C、B,与直线![]() 相交于点A.
相交于点A.
(1)求A点坐标;
(2)如果在y轴上存在一点P,使△OAP是以OA为底边的等腰三角形,求P点坐标;
(3)在直线![]() 上是否存在点Q,使△OAQ的面积等于6?若存在,请求出Q点的坐标,若不存在,请说明理由.
上是否存在点Q,使△OAQ的面积等于6?若存在,请求出Q点的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在长方形ABCD内,将两张边长分别为a和b(a>b)的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),长方形中未被这两张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为S1,图2中阴影部分的面积为S2.当AD﹣AB=2时,S2﹣S1的值为_______.(用a、b的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C是线段AB的中点.
(1)若点D在CB上,且DB=2cm,AD=8cm,求线段CD的长度;
![]()
(2)若将(1)中的“点D在CB上”改为“点D在CB的延长线上”,其它条件不变,请画出相应的示意图,并求出此时线段CD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
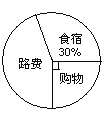
【题目】韦魏一家三口随旅游团支九寨沟旅游,韦魏把旅途费用支出情况制成了如下的统计图,若他们共花费人民币8600元,
⑴哪一部分的费用占整个支出的![]() ,花费了多少元?
,花费了多少元?
⑵在食宿上花费了多少元?
⑶这一家往返的路费占总支出的百分之几?花费了多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=![]() x-15的图象与x轴,y轴分别交于点A,B,O为坐标原点,则在△OAB内部(包括边界),纵坐标、横坐标都是整数的点(整点)共有_________个.
x-15的图象与x轴,y轴分别交于点A,B,O为坐标原点,则在△OAB内部(包括边界),纵坐标、横坐标都是整数的点(整点)共有_________个.
查看答案和解析>>
科目:初中数学 来源: 题型:
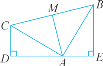
【题目】如图,已知∠CDA=∠AEB=90°,且CD=AE,AD=BE.
(1)求证:AC=BA.
(2)△ABC是什么三角形?请说明理由.
(3)如果AM⊥BC,那么AM=![]() BC吗?请说明理由.
BC吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
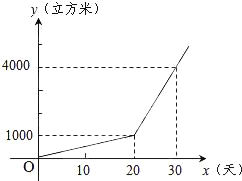
【题目】某农户种植一种经济作物,总用水量y(米3)与种植时间x(天)之间的函数关系式如图所示.
(1)第20天的总用水量为多少米3?
(2)当x≥20时,求y与x之间的函数关系式;
(3)种植时间为多少天时,总用水量达到7000米3?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com