
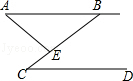
 如图,AB∥CD,∠A=46°,∠C=27°,则∠AEC的大小应为73°.
如图,AB∥CD,∠A=46°,∠C=27°,则∠AEC的大小应为73°.  名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:选择题
| A. | y=(x-3)2-4 | B. | y=(x+3)2-4 | C. | y=(x-3)2+5 | D. | y=(x-3)2+14 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
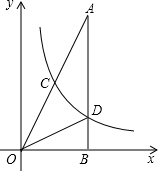 如图,在△AOB中,∠ABO=90°,OB=4,AB=8,反比例函数y=$\frac{k}{x}$在第一象限内的图象分别交OA,AB于点C和点D,且△BOD的面积S△BOD=4.
如图,在△AOB中,∠ABO=90°,OB=4,AB=8,反比例函数y=$\frac{k}{x}$在第一象限内的图象分别交OA,AB于点C和点D,且△BOD的面积S△BOD=4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
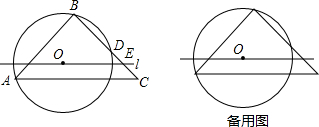
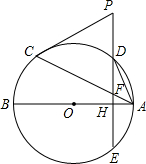 如图,AB、AC分别是⊙O的直径和弦,点D为劣弧AC上一点,弦DE⊥AB分别交⊙O于E,交AB于H,交AC于F.P是ED延长线上一点且PC=PF.
如图,AB、AC分别是⊙O的直径和弦,点D为劣弧AC上一点,弦DE⊥AB分别交⊙O于E,交AB于H,交AC于F.P是ED延长线上一点且PC=PF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
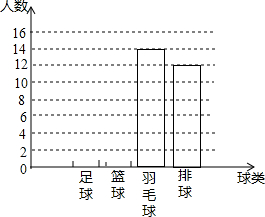 为了了解某校学生对球类运动的爱好情况,采用抽样的方法,从足球、篮球、羽毛球、排球等四个方面调查了若干名学生,并绘制成不完整的条形图.已知最喜欢篮球的人数占调查人数的32%,最喜欢排球的人数是最喜欢足球人数的1.5倍.
为了了解某校学生对球类运动的爱好情况,采用抽样的方法,从足球、篮球、羽毛球、排球等四个方面调查了若干名学生,并绘制成不完整的条形图.已知最喜欢篮球的人数占调查人数的32%,最喜欢排球的人数是最喜欢足球人数的1.5倍.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com