
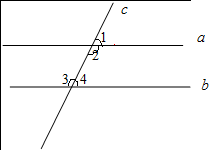
 如图,因为a∥b,所以∠1=∠4,理由是两直线平行,同位角相等.
如图,因为a∥b,所以∠1=∠4,理由是两直线平行,同位角相等. 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:选择题
 小王把一张矩形纸片沿BC折叠,顶点A落在点A′,再过点A′折叠使折痕DE∥BC,若AB=4,AC=3,则△ADE的面积是( )
小王把一张矩形纸片沿BC折叠,顶点A落在点A′,再过点A′折叠使折痕DE∥BC,若AB=4,AC=3,则△ADE的面积是( )| A. | 24 | B. | 30 | C. | 60 | D. | 90 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 车型 | 甲 | 乙 | 丙 |
| 汽车运载量(吨/辆) | 5 | 8 | 10 |
| 汽车运费(元/辆) | 400 | 500 | 600 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com