
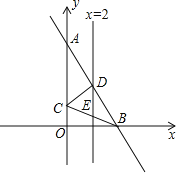
【题目】如图,平面直角坐标系中,直线AB:y=-2x+8交y轴于点A,交x轴于点B,以AB为底作等腰三角形△ABC的顶点C恰好落在y轴上,连接BC,直线x=2交AB于点D,交BC于点E,交x轴于点G,连接CD.
(1)求证:∠OCB=2∠CBA;
(2)求点C的坐标和直线BC的解析式;
(3)求△DEB的面积;
(4)在x轴上存在一点P使PD-PC最长,请直接写出点P的坐标.
【答案】(1)证明见解析;(2)C(0,3),直线BC解析式为y=-![]() x+3;(3)
x+3;(3)![]() ;(4)P(-6,0).
;(4)P(-6,0).
【解析】
(1)利用等腰三角形的性质和外角的性质可证得结论;
(2)可先求得A、B的坐标,则可求得OA=8、OB=4,在设OC=x,则AC=BC=8-x,在Rt△OBC中由勾股定理可列方程,可求得OC的长,则可求得点C的坐标,再利用待定系数法可求得直线BC的解析式;
(3)由直线AB、BC的解析式可分别求得点D、E的坐标,则可求得DE的长,可求得△DEB的面积;
(4)利用三角形三边关系可知PD-PC<CD,当P、D、C三点在一条线上时,则有PD-PC=CD,此时其差最长,延长CD交x轴于点P,则该点即为P点,由C、D的坐标可求得直线CD的解析式,则可求得点P的坐标.
(1)证明:
∵△ABC为等腰三角形,
∴∠CAB=∠CBA,∠OCB为外角,
∴∠OCB=∠CAB+∠CBA,
∴∠OCB=2∠CBA;
(2)在y=-2x+8中,令x=0可得y=8,令y=0可求得x=4,
∴A(0,8),B(4,0),
∴OA=8,OB=4,
设OC=x,则AC=BC=8-x,
在Rt△OBC中,由勾股定理可得BC2=OC2+OB2,
即(8-x)2=x2+42,解得x=3,
∴C(0,3),
设直线BC解析式为y=kx+b,
把B、C点的坐标代入可得
![]() ,解得
,解得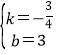 ,
,
∴直线BC解析式为y=-![]() x+3;
x+3;
(3)直线x=2交AB于点D,交BC于点E,交x轴于点G,
∴D(2,4),E(2,![]() ),G(2,0),
),G(2,0),
∴DE=4-![]() =
=![]() ,且B(4,0),
,且B(4,0),
∴BG=4-2=2,
∴S△DEB=![]() DEBG=
DEBG=![]() ×
×![]() ×2=
×2=![]() ;
;
(4)∵PD-PC<CD,
∴当P、D、C三点在一条线上时,则有PD-PC=CD,此时其差最长,
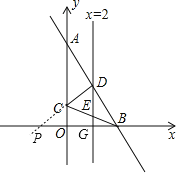
延长CD交x轴于点P,则该点即为P点,
设直线CD解析式为y=mx+n,
把C、D坐标代入可得![]() ,解得
,解得![]() ,
,
∴直线CD解析式为y=![]() x+3,
x+3,
令y=0可得![]() x+3=0,解得x=-6,
x+3=0,解得x=-6,
∴P(-6,0).


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】某校墙边有两根木杆.
(1)某一时刻甲木杆在阳光下的影子如图所示,你能画出乙木杆的影子吗?(用线段表示影子)
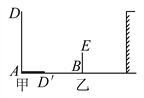
(2)当乙木杆移动到什么位置时,其影子刚好不落在墙上?
(3)在你所画的图中有相似三角形吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 的图像与
的图像与![]() 轴、
轴、![]() 轴分别交于点B、A.以AB为边在第一象限内作等腰直角三角形ABC,且∠ABC=90°,BA=BC,作OB的垂直平分线l,交直线AB与点E,交x轴于点G.
轴分别交于点B、A.以AB为边在第一象限内作等腰直角三角形ABC,且∠ABC=90°,BA=BC,作OB的垂直平分线l,交直线AB与点E,交x轴于点G.
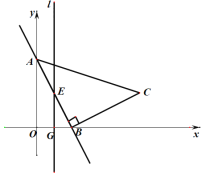
(1)求点![]() 的坐标;
的坐标;
(2)在OB的垂直平分线l上有一点M,且点M与点C位于直线AB的同侧,使得![]() ,求点M的坐标;
,求点M的坐标;
(3)在(2)的条件下,联结CE、CM,判断△CEM的形状,并给予证明;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠A=∠D=90°,点E、F在线段BC上,DE与AF交于点O,且AB=DC,BE=CF.求证:
(1)AF=DE
(2)若OP⊥EF,求证:OP平分∠EOF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在方格纸中(小正方形的边长为1),反比例函数y=![]() 与直线的交点A、B均在格点上,根据所给的直角坐标系(O是坐标原点),解答下列问题:
与直线的交点A、B均在格点上,根据所给的直角坐标系(O是坐标原点),解答下列问题:
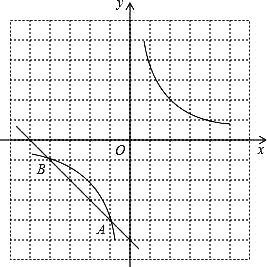
(1)分别写出点A、B的坐标后,把直线AB向右平移5个单位,再向上平移5个单位,画出平移后的直线A′B′;
(2)若点C在函数y=![]() 的图象上,△ABC是以AB为底的等腰三角形,请写出点C的坐标.
的图象上,△ABC是以AB为底的等腰三角形,请写出点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用洗衣粉洗衣物时,漂洗的次数与衣物中洗衣粉的残留量近似地满足反比例函数关系,寄宿生小红和小敏晚饭后用同一种洗衣粉各自洗一件同样的衣服,漂洗时,小红每次用一盆水(约10升),小敏每次用半盆水(约5升).如果她们都用了5克洗衣粉,第一次漂洗后,小红的衣服中残留的洗衣粉还有1.5克,小敏的衣服中残留的洗衣粉还有2克.
(1)请帮助小红和小敏求出各自衣服中洗衣粉的残留量y与漂洗次数x之间的函数关系式
(2)当洗衣粉的残留量降至0.5克时,便视为衣服漂洗干净,从节约用水的角度来看,你认为谁的漂洗方法值得提倡?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
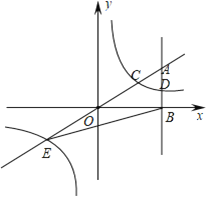
【题目】如图,在平面直角坐标系中,A点的坐标为(a,6),AB⊥x轴于点B,![]() =
=![]() ,反比例函数y=
,反比例函数y=![]() 的图象的一支分别交AO、AB于点C、D.延长AO交反比例函数的图象的另一支于点E.已知点D的纵坐标为
的图象的一支分别交AO、AB于点C、D.延长AO交反比例函数的图象的另一支于点E.已知点D的纵坐标为![]() .
.
(1)求反比例函数的解析式及点E的坐标;
(2)连接BC,求S△CEB.
(3)若在x轴上的有两点M(m,0)N(-m,0).
①以E、M、C、N为顶点的四边形能否为矩形?如果能求出m的值,如果不能说明理由.
②若将直线OA绕O点旋转,仍与y=![]() 交于C、E,能否构成以E、M、C、N为顶点的四边形为菱形,如果能求出m的值,如果不能说明理由.
交于C、E,能否构成以E、M、C、N为顶点的四边形为菱形,如果能求出m的值,如果不能说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一束光线从点A(3,3)出发,经过y轴上点C反射后经过点B(1,0),则光线从A点到B点经过的路线长是( )
A. 4B. 5C. 6D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“垃圾不落地,商南更美丽”。某中学为了了解七年级学生对这个一倡议的落实情况,学校安排政教处在七年级学生中随机抽取了部分学生,并针对学生“是否随手丢垃圾”这一情况进行了问卷调查,将这一情况分为:![]() ——从不随手丢垃圾;
——从不随手丢垃圾;![]() ——偶尔随手丢垃圾;
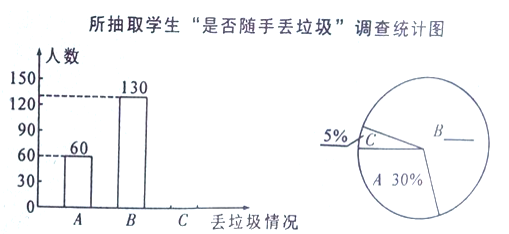
——偶尔随手丢垃圾;![]() ——经常随手丢垃圾三项。要求每位被调查的学生必须从以上三项中选一项且只能选一项。现将调查结果绘制成以下两幅不完整的统计图。请你根据以上信息,解答下列问题:
——经常随手丢垃圾三项。要求每位被调查的学生必须从以上三项中选一项且只能选一项。现将调查结果绘制成以下两幅不完整的统计图。请你根据以上信息,解答下列问题:
(1)补全条形统计图和扇形统计图;
(2)图中“偶尔随手丢垃圾”所在扇形的圆心角为______________;
(3)若该校七年级共有1500名学生,请你估计该年级学生中“经常随手丢垃圾”的学生约有多少人?谈谈你的看法?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com