
【题目】如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接BE.
(1)求证:BE与⊙O相切;
(2)设OE交⊙O于点F,若DF=1,BC=2![]() ,求阴影部分的面积.
,求阴影部分的面积.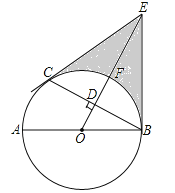
【答案】(1)证明见解析;(2)4![]() ﹣
﹣![]() π.
π.
【解析】试题分析:(1)连接OC,如图,利用切线的性质得∠OCE=90°,再根据垂径定理得到CD=BD,则OD垂中平分BC,所以EC=EB,接着证明△OCE≌△OBE得到∠OBE=∠OCE=90°,然后根据切线的判定定理得到结论;
(2)设⊙O的半径为r,则OD=r﹣1,利用勾股定理得到(r﹣1)2+(![]() )2=r2,解得r=2,再利用三角函数得到∠BOD=60°,则∠BOC=2∠BOD=120°,接着计算出BE=
)2=r2,解得r=2,再利用三角函数得到∠BOD=60°,则∠BOC=2∠BOD=120°,接着计算出BE=![]() OB=2
OB=2![]() ,
,
然后根据三角形面积公式和扇形的面积公式,利用阴影部分的面积=2S△OBE﹣S扇形BOC进行计算即可.
试题解析:(1)证明:连接OC,如图,
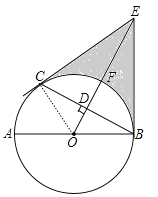
∵CE为切线,
∴OC⊥CE,
∴∠OCE=90°,
∵OD⊥BC,
∴CD=BD,
即OD垂中平分BC,
∴EC=EB,
在△OCE和△OBE中
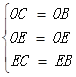 ,
,
∴△OCE≌△OBE,
∴∠OBE=∠OCE=90°,
∴OB⊥BE,
∴BE与⊙O相切;
(2)解:设⊙O的半径为r,则OD=r﹣1,
在Rt△OBD中,BD=CD=![]() BC=
BC=![]() ,
,
∴(r﹣1)2+(![]() )2=r2,解得r=2,
)2=r2,解得r=2,
∵tan∠BOD=![]() =
=![]() ,
,
∴∠BOD=60°,
∴∠BOC=2∠BOD=120°,
在Rt△OBE中,BE=![]() OB=2
OB=2![]() ,
,
∴阴影部分的面积=S四边形OBEC﹣S扇形BOC
=2S△OBE﹣S扇形BOC
=2×![]() ×2×2
×2×2![]() ﹣
﹣![]()
![]()
=4![]() ﹣
﹣![]() π.
π.


科目:初中数学 来源: 题型:
【题目】根据下列事件发生的概率,把A,B,C,D填入事件后的括号里.
A.发生的概率为0 B.发生的概率小于![]()
C.发生的概率大于![]() D.发生的概率为1
D.发生的概率为1
(1)从一副扑克牌中任意抽取一张,是红桃;( )
(2)2024年2月有29天;( )
(3)小波能举起500 kg的大石头;( )
(4)从5张分别写有数字1,2,4,6,8的卡片中任取一张,卡片上数字恰为偶数.( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】推理填空:如图:
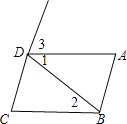
![]() 若
若![]() ,
,
则______ ![]() ______
______ ![]() 内错角相等,两直线平行
内错角相等,两直线平行![]() ;
;
若![]() ,
,
则______ ![]() ______
______ ![]() 同旁内角互补,两直线平行
同旁内角互补,两直线平行![]() ;
;
![]() 当______
当______ ![]() ______ 时,
______ 时,
![]() 两直线平行,同旁内角互补
两直线平行,同旁内角互补![]() ;
;
![]() 当______
当______ ![]() ______ 时,
______ 时,
![]()
![]() 两直线平行,同位角相等
两直线平行,同位角相等![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一不透明的布袋里,装有红、黄、蓝三种颜色的小球(除颜色外其余都相同),其中有红球2个,蓝球1个,黄球若干个,现从中任意摸出一个球是红球的概率为![]()
(1)求口袋中黄球的个数;
(2)甲同学先随机摸出一个小球(不放回),再随机摸出一个小球,请用“树状图法”或“列表法”,求两次摸出都是红球的概率;
(3)现规定:摸到红球得5分,摸到黄球得3分,摸到蓝球得2分(每次摸后放回),乙同学在一次摸球游戏中,第一次随机摸到一个红球第二次又随机摸到一个蓝球,若随机再摸一次,求乙同学三次摸球所得分数之和不低于10分的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次物理竞赛中,有一道四选二的双项选择题,评分标准是:多选或只要选错一项就不得分,只选一项且对得1分,全对得3分.
(1)小娟在不会做的情况下,根据题意决定任选一项作为答案,求她得到1分的概率.
(2)小娜在不会做的情况下,根据题意决定任选两项作答案,用列表法表示小娜答案的所有可能结果,并求她得到3分的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CN是等边△![]() 的外角
的外角![]() 内部的一条射线,点A关于CN的对称点为D,连接AD,BD,CD,其中AD,BD分别交射线CN于点E,P.
内部的一条射线,点A关于CN的对称点为D,连接AD,BD,CD,其中AD,BD分别交射线CN于点E,P.
(1)依题意补全图形;
(2)若![]() ,求
,求![]() 的大小(用含
的大小(用含![]() 的式子表示);
的式子表示);
(3)用等式表示线段![]() ,
, ![]() 与
与![]() 之间的数量关系,并证明.
之间的数量关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于0,1以及真分数p,q,r,若p<q<r,我们称q为p和r的中间分数.为了帮助我们找中间分数,制作了下表:

两个不等的正分数有无数多个中间分数.例如:上表中第③行中的3个分数![]() 、
、![]() 、
、![]() ,有
,有![]() ,所以
,所以![]() 为
为![]() 和
和![]() 的一个中间分数,在表中还可以找到
的一个中间分数,在表中还可以找到![]() 和
和![]() 的中间分数
的中间分数![]() ,
, ![]() ,
, ![]() ,
, ![]() .把这个表一直写下去,可以找到
.把这个表一直写下去,可以找到![]() 和
和![]() 更多的中间分数.
更多的中间分数.
(1)按上表的排列规律,完成下面的填空:
①上表中括号内应填的数为 ;
②如果把上面的表一直写下去,那么表中第一个出现的![]() 和
和![]() 的中间分数是 ;
的中间分数是 ;
(2)写出分数![]() 和
和![]() (a、b、c、d均为正整数,
(a、b、c、d均为正整数, ![]() ,
, ![]() )的一个中间分数(用含a、b、c、d的式子表示),并证明;
)的一个中间分数(用含a、b、c、d的式子表示),并证明;
(3)若![]() 与
与![]() (m、n、s、 t均为正整数)都是
(m、n、s、 t均为正整数)都是![]() 和
和![]() 的中间分数,则
的中间分数,则![]() 的最小值为 .
的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
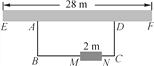
【题目】如图,利用一面墙(墙EF最长可利用28米),围成一个矩形花园ABCD.与墙平行的一边BC上要预留2米宽的入口(如图中MN所示,不用砌墙).现有砌60米长的墙的材料.
(1)当矩形的长BC为多少米时,矩形花园的面积为300平方米;
(2)能否围成480平方米的矩形花园,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,(1)已知∠ABC,射线ED∥AB,过点E作∠DEF=∠ABC,试说明BC∥EF;
(2)如图②,已知∠ABC,射线ED∥AB,∠ABC+∠DEF=180°.判断直线BC与直线EF的位置关系,并说明理由;
(3)根据以上探究,你发现了一个什么结论?请你写出来;
(4)如图③,已知AC⊥BC,CD⊥AB,DE⊥AC,HF⊥AB,若∠1=48°,试求∠2的度数.



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com