
 ��MN=2
��MN=2 ��
�� ���ӻ�������EF=5���ѡ�OBC����ƽ�ơ���ת�����Ʊ任��ʹ������������ֱ����E��F�غϣ���EF��ͬһ�࣬�����������ι��ж��ٸ��������������ҳ���һ�������ڡ�O�ϵ�������������ͼ�л�����������Σ������������������OBC���ܳ�֮�ȣ�
���ӻ�������EF=5���ѡ�OBC����ƽ�ơ���ת�����Ʊ任��ʹ������������ֱ����E��F�غϣ���EF��ͬһ�࣬�����������ι��ж��ٸ��������������ҳ���һ�������ڡ�O�ϵ�������������ͼ�л�����������Σ������������������OBC���ܳ�֮�ȣ�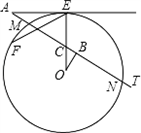
| �⣺��1����AE�С�O�ڵ�E�� ��AE��CE����OB��AT�� ���AEC=��CBO=90�㣬 �֡�BCO=��ACE�� ���AEC�ס�OBC���֡�A=30�㣬 ���COB=��A=30�㣻 ��2����AE=3  ����A=30�㣬 ����A=30�㣬����Rt��AEC�У�tanA=tan30��=  ����EC=AEtan30��=3�� ����EC=AEtan30��=3����OB��MN�� ��BΪMN���е㣬��MN=2  �� ����MB=  MN= MN=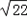 �� ������OM���ڡ�MOB�У�OM=R��MB=  �� ����OB=  = = �� ���ڡ�COB�У���BOC=30�㣬 ��cos��BOC=cos30��=  = = �� ����BO=  OC�� OC����OC=  OB= OB=  �� ����OC+EC=OM=R�� ��R=   +3�� +3�������ã�R2+18R��115=0�� ����R+23����R��5��=0�� ��ã�R=��23����ȥ����R=5�� ��R=5�� ��3����EFͬһ�࣬��COB����ƽ�ơ���ת�����Ʊ任�� ��������������6���� ��ͼ��ÿСͼ2����������Բ�ϵ������Σ�����ͼ��ʾ�� �ӳ�EO��ԲO�ڵ�D������DF�� ��ͼ��ʾ�� ��EF=5��ֱ��ED=10���ɵó���FDE=30�㣬 ��FD=5  �� ����C��EFD=5+10+5  =15+5 =15+5 �� ���ɣ�2���ɵ�C��COB=3+  �� ����C��EFD��C��COB=��15+5  ������3+ ������3+ ��=5��1�� ��=5��1�� |
|


 �����Ƹ���ʦ����ϵ�д�
�����Ƹ���ʦ����ϵ�д� ��ͨ����ͬ����ϰ��ϵ�д�
��ͨ����ͬ����ϰ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 3 |
 ��MN=2
��MN=2| 22 |
 |
| FME |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������һ����顡���꼶��ѧ���ϡ������հ�α걾�� ���հ�α걾 ���ͣ�013
��ͼ��AE�С�O�ڵ�E��AC��CD��DB��10�����߶�AE�ij�Ϊ

A��![]()
B��15
C��![]()
D��20
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2012���㽭ʡ�������п���ѧ�Ծ� ���ͣ�044
��ͼ��AE�С�O�ڵ�E��AT����O�ڵ�M��N���߶�OE��AT�ڵ�C��OB��AT�ڵ�B����֪��EAT��30�㣬AE��3![]() ��MN��2
��MN��2![]() ��
��

(1)���COB�Ķ�����
(2)���O�İ뾶R��
(3)��F�ڡ�O��(![]() ���ӻ�)����EF��5���ѡ�OBC����ƽ�ơ���ת�����Ʊ任��ʹ������������ֱ����E��F�غϣ���EF��ͬһ�࣬�����������ι��ж��ٸ��������������ҳ���һ�������ڡ�O�ϵ�������������ͼ�л�����������Σ������������������OBC���ܳ�֮�ȣ�
���ӻ�)����EF��5���ѡ�OBC����ƽ�ơ���ת�����Ʊ任��ʹ������������ֱ����E��F�غϣ���EF��ͬһ�࣬�����������ι��ж��ٸ��������������ҳ���һ�������ڡ�O�ϵ�������������ͼ�л�����������Σ������������������OBC���ܳ�֮�ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2012���㽭ʡ�������п���ѧ�Ծ��������棩 ���ͣ������
 ��MN=2
��MN=2 ��
�� ���ӻ�������EF=5���ѡ�OBC����ƽ�ơ���ת�����Ʊ任��ʹ������������ֱ����E��F�غϣ���EF��ͬһ�࣬�����������ι��ж��ٸ��������������ҳ���һ�������ڡ�O�ϵ�������������ͼ�л�����������Σ������������������OBC���ܳ�֮�ȣ�
���ӻ�������EF=5���ѡ�OBC����ƽ�ơ���ת�����Ʊ任��ʹ������������ֱ����E��F�غϣ���EF��ͬһ�࣬�����������ι��ж��ٸ��������������ҳ���һ�������ڡ�O�ϵ�������������ͼ�л�����������Σ������������������OBC���ܳ�֮�ȣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com