
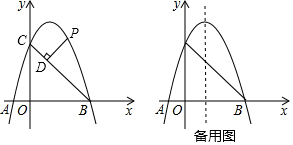
 如图,是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=5米,AB=7米,∠MAD=45°,∠MBC=30°,求警示牌的高CD为多少米?(结果保留根号)
如图,是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=5米,AB=7米,∠MAD=45°,∠MBC=30°,求警示牌的高CD为多少米?(结果保留根号) 科目:初中数学 来源: 题型:解答题
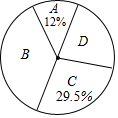 某区为了解七年级学生开展跳绳活动的情况,随机调查了该区部分学校七年级学生1分钟跳绳的次数,将调查结果进行统计,下面是根据调查数据制作的统计图表的一部分.
某区为了解七年级学生开展跳绳活动的情况,随机调查了该区部分学校七年级学生1分钟跳绳的次数,将调查结果进行统计,下面是根据调查数据制作的统计图表的一部分.| 分组 | 次数x(个) | 人数 |
| A | 0≤x<120 | 24 |
| B | 120≤x<130 | 72 |
| C | 130≤x<140 | |
| D | x≥140 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com