
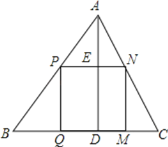
ĄŸÌâÄżĄżÓĂÒ»žöŽóĐĄĐÎŚŽč̶š”ÄČ»”ȱßÈńœÇÈęœÇĐÎÖœŁŹŒôłöÒ»žöŚîŽó”ÄŐę·œĐÎÖœ±žÓĂŁźŒŚÍŹŃ§Ë”ŁșĄ°”±Őę·œĐΔÄÒ»±ßÔڌ±ßʱŁŹŒôłö”ÄÄÚœÓŐę·œĐÎŚîŽóĄ±Ł»ÒÒ͏ѧ˔ŁșĄ°”±Őę·œĐΔÄÒ»±ßÔÚŚî¶Ì±ßÉÏʱŁŹŒôłö”ÄÄÚœÓŐę·œĐÎŚîŽóĄ±Ł»±û͏ѧ˔ŁșĄ°Č»È·¶šŁŹŒôČ»łöŐâŃù”ÄŐę·œĐÎÖœŁźĄ±ÄăÈÏÎȘËË””ÄÓĐ”ÀÀíŁŹÇëրÜŁźŁšŒÙÉèÍŒÖĐĄśABC”ÄÈę±ßaŁŹbŁŹcŁŹÇÒaŁŸbŁŸcŁŹÈę±ßÉϔĞ߷ֱđŒÇÎȘhaŁŹhbŁŹhcŁ©
ĄŸŽđ°žĄżÒÒ͏ѧ˔”ÄŐęÈ·ŁŹŒûœâÎö
ĄŸœâÎöĄż
ÉèĄśABC”ÄÈęÌő±ßÉϔĶÔÓŠžß·Ö±đÎȘhaŁŹhbŁŹhcŁŹÒ»±ß·Ö±đÂäÔÚaŁŹbŁŹcÉÏ”ÄÄÚœÓŐę·œĐα߳€·Ö±đŒÇÎȘxaŁŹxbŁŹxcŁŹÀûÓĂÏàËÆÈęœÇĐÎĐÔÖÊżÉ”Ă![]() ŁŹœű¶ű±íÊŸłöxaŁœ
ŁŹœű¶ű±íÊŸłöxaŁœ![]() ŁŹÍŹÀíxbŁœ
ŁŹÍŹÀíxbŁœ![]() ŁŹxcŁœ
ŁŹxcŁœ![]() ŁŹÈ»șóœ«ËüĂÇŚśČÓë0±ÈœÏŁŹœű¶ű”ĂłöxaŁŹxbŁŹxcŁŹ”ÄŽóĐĄčŰÏ”Łź
ŁŹÈ»șóœ«ËüĂÇŚśČÓë0±ÈœÏŁŹœű¶ű”ĂłöxaŁŹxbŁŹxcŁŹ”ÄŽóĐĄčŰÏ”Łź
ÉèĄśABC”ÄÈęÌő±ßÉϔĶÔÓŠžß·Ö±đÎȘhaŁŹhbŁŹhcŁŹÒ»±ß·Ö±đÂäÔÚaŁŹbŁŹcÉÏ”ÄÄÚœÓŐę·œĐα߳€·Ö±đŒÇÎȘxaŁŹxbŁŹxcŁŹ
ÒŚ”ĂŁșĄśAPN~ĄśABCŁŹ
Ąà![]() ŁŹ
ŁŹ
ĄàxaŁœ![]() ŁŹ
ŁŹ
ÍŹÀíxbŁœ![]() ŁŹxcŁœ
ŁŹxcŁœ![]() ŁŹ
ŁŹ
ÓÖÉèÈęœÇĐÎABCĂæ»ęÎȘs
Ąàxa©xbŁœ![]()
=![]()
=
=![]() (
(![]()
=![]() )
)
ĄßaŁŸbŁŹhaŁŒbŁŹ
ĄàŁšb©aŁ©Łš1©![]() Ł©ŁŒ0ŁŹ
Ł©ŁŒ0ŁŹ
ŒŽxa©xbŁŒ0ŁŹ
ĄàxaŁŒxbŁŹ
ÍŹÀíŁșxbŁŒxcŁŹ
ĄàxaŁŒxbŁŒxcŁź
ĄàÒÒ͏ѧ˔”ÄŐęÈ·Łź



| Äꌶ | žßÖĐżÎłÌ | Äꌶ | łőÖĐżÎłÌ |
| žßÒ» | žßÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ | łőÒ» | łőÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ |
| žß¶ț | žß¶țĂâ·ŃżÎłÌÍÆŒöŁĄ | łő¶ț | łő¶țĂâ·ŃżÎłÌÍÆŒöŁĄ |
| žßÈę | žßÈęĂâ·ŃżÎłÌÍÆŒöŁĄ | łőÈę | łőÈęĂâ·ŃżÎłÌÍÆŒöŁĄ |
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒąÙŁŹÔÚŸŰĐÎ![]() ÖĐŁŹÒŃÖȘ
ÖĐŁŹÒŃÖȘ![]() ŁŹ”ă
ŁŹ”ă![]() ÎȘ
ÎȘ![]() ±ßÉÏÒ»”㣏ÂúŚă
±ßÉÏÒ»”㣏ÂúŚă![]() ŁŹ¶Ż”ă
ŁŹ¶Ż”ă![]() ÒÔ
ÒÔ![]() ”ÄËÙ¶ÈŃŰÏ߶Î
”ÄËÙ¶ÈŃŰÏ߶Î![]() ŽÓ”ă
ŽÓ”ă![]() ÒƶŻ”œ”ă
ÒƶŻ”œ”ă![]() ŁŹÁŹœÓ
ŁŹÁŹœÓ![]() ŁŹŚś
ŁŹŚś![]() ŁŹœ»Ï߶Î
ŁŹœ»Ï߶Î![]() ÓÚ”ă
ÓÚ”ă![]() ŁŹÉè”ă
ŁŹÉè”ă![]() ÒƶŻ”ÄʱŒäÎȘ
ÒƶŻ”ÄʱŒäÎȘ![]() ŁŹ
ŁŹ![]() ”Äł€¶ÈÎȘ
”Äł€¶ÈÎȘ![]() ŁŹ
ŁŹ![]() Óë
Óë![]() ”ÄșŻÊęčŰÏ”ÈçÍŒąÚËùÊŸ.
”ÄșŻÊęčŰÏ”ÈçÍŒąÚËùÊŸ.
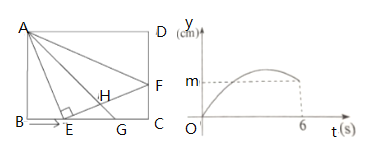
Łš1Ł©ÍŒąÙÖĐŁŹ![]() _______
_______![]() ŁŹÍŒąÚÖĐŁŹ
ŁŹÍŒąÚÖĐŁŹ![]() _______Ł»
_______Ł»
Łš2Ł©”ă![]() ÄÜ·ńÎȘÏ߶Î
ÄÜ·ńÎȘÏ߶Î![]() ”ÄÖД㣿ÈôżÉÄÜŁŹÇółöŽËʱ
”ÄÖД㣿ÈôżÉÄÜŁŹÇółöŽËʱ![]() ”ÄÖ”ŁŹÈôČ»żÉÄÜŁŹÇë˔ÜÀíÓÉŁ»
”ÄÖ”ŁŹÈôČ»żÉÄÜŁŹÇë˔ÜÀíÓÉŁ»
Łš3Ł©ÔÚÍŒąÙÖĐŁŹÁŹœÓ![]() Ąą
Ąą![]() ŁŹÉè
ŁŹÉè![]() Óë
Óë![]() œ»ÓÚ”ă
œ»ÓÚ”ă![]() ŁŹÈô
ŁŹÈô![]() Æœ·Ö
Æœ·Ö![]() ”ÄĂæ»ęŁŹÇóŽËʱ
”ÄĂæ»ęŁŹÇóŽËʱ![]() ”ÄÖ”.
”ÄÖ”.
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
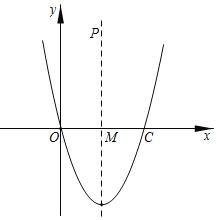
ĄŸÌâÄżĄżÒŃÖȘĆŚÎïÏ߶„”ăŚű±êÎȘŁš2ŁŹ©4Ł©ŁŹÇÒÓëxÖ᜻ÓÚÔ”ășÍ”ăCŁŹ¶ÔłÆÖáÓëxÖ᜻”ăÎȘMŁź
Łš1Ł©ÇóĆŚÎïÏߔĜâÎöÊœŁ»
Łš2Ł©A”ăÔÚĆŚÎïÏßÉÏŁŹÇÒA”ă”ÄșáŚű±êÎȘ©2ŁŹÔÚĆŚÎïÏ߶ԳÆÖáÉÏŐÒÒ»”ăBŁŹÊč”ĂABÓëCB”ÄČîŚîŽóŁŹÇóB”ă”ÄŚű±êŁ»
Łš3Ł©P”ăÔÚĆŚÎïÏߔĶԳÆÖáÉÏŁŹÇÒP”ă”ÄŚĘŚű±êÎȘ8ŁźÌœŸżŁșÔÚĆŚÎïÏßÉÏÊÇ·ńŽæÔÚ”ăQÊč”ĂOĄąMĄąPĄąQËÄ”ăčČÔČŁŹÈôŽæÔÚÇółöQ”ăŚű±êŁ»ÈôČ»ŽæÔÚÇë˔ÜÀíÓÉŁź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒ,ÔÚÆœĂæÖ±œÇŚű±êÏ”ÖĐ,ËıßĐÎ![]() ”Ķ„”ă
”Ķ„”ă![]() ÊÇŚű±êԔ㣏”ă
ÊÇŚű±êԔ㣏”ă![]() ÔÚ”ÚÒ»ÏóÏȚ,”ă
ÔÚ”ÚÒ»ÏóÏȚ,”ă![]() ÔÚ”ÚËÄÏóÏȚ,”ă
ÔÚ”ÚËÄÏóÏȚ,”ă![]() ÔÚ
ÔÚ![]() Öá”ÄŐę°ëÖáÉÏŁŹ
Öá”ÄŐę°ëÖáÉÏŁŹ![]() ÇÒ
ÇÒ![]() .
.
(1)Çó”ă![]() șÍ”ă
șÍ”ă![]() ”ÄŚű±ê;
”ÄŚű±ê;
(2)”ă![]() ÊÇÏ߶Î
ÊÇÏ߶Î![]() ÉÏ”ÄÒ»žö¶Ż”ă(”ă
ÉÏ”ÄÒ»žö¶Ż”ă(”ă![]() Č»Óë”ă
Č»Óë”ă![]() ÖŰșÏ) ,ÒÔĂżĂë
ÖŰșÏ) ,ÒÔĂżĂë![]() žö”„λ”ÄËÙ¶ÈÓÉ”ă
žö”„λ”ÄËÙ¶ÈÓÉ”ă![]() Ïò”ă
Ïò”ă![]() Ô˶ŻŁŹčę”ă
Ô˶ŻŁŹčę”ă![]() ”ÄÖ±Ïß
”ÄÖ±Ïß![]() Óë
Óë![]() ÖáÆœĐĐ,Ö±Ïß
ÖáÆœĐĐ,Ö±Ïß![]() œ»±ß
œ»±ß![]() »ò±ß
»ò±ß![]() ÓÚ”ă
ÓÚ”ă![]() ,œ»±ß
,œ»±ß![]() »ò±ß
»ò±ß![]() ÓÚ”ă
ÓÚ”ă![]() ,Éè”ă
,Éè”ă![]() .Ô˶ŻÊ±ŒäÎȘ
.Ô˶ŻÊ±ŒäÎȘ![]() ,Ï߶Î
,Ï߶Î![]() ”Äł€¶ÈÎȘ
”Äł€¶ÈÎȘ![]() ,ÒŃÖȘ
,ÒŃÖȘ![]() ʱ,Ö±Ïß
ʱ,Ö±Ïß![]() ÇĄșĂčę”ă
ÇĄșĂčę”ă![]() .
.
ąÙ”±![]() ʱ,Çó
ʱ,Çó![]() čŰÓÚ
čŰÓÚ![]() ”ÄșŻÊęčŰϔʜ;
”ÄșŻÊęčŰϔʜ;
ąÚ”ă![]() łö·ąÊ±”ă
łö·ąÊ±”ă![]() ÒČŽÓ”ă
ÒČŽÓ”ă![]() łö·ą,ÒÔĂżĂë
łö·ą,ÒÔĂżĂë![]() žö”„λ”ÄËÙ¶ÈÏò”ă
žö”„λ”ÄËÙ¶ÈÏò”ă![]() Ô˶ŻŁŹ”ă
Ô˶ŻŁŹ”ă![]() ÍŁÖčʱ”ă
ÍŁÖčʱ”ă![]() ÒČÍŁÖč.Éè
ÒČÍŁÖč.Éè![]() ”ÄĂæ»ęÎȘ
”ÄĂæ»ęÎȘ![]() ,Çó
,Çó![]() Óë
Óë![]() ”ÄșŻÊęčŰϔʜ;
”ÄșŻÊęčŰϔʜ;
ąÛÖ±œÓĐŽłöąÚÖĐ![]() ”ÄŚîŽóÖ”ÊÇ .
”ÄŚîŽóÖ”ÊÇ .
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
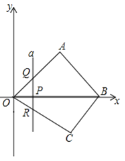
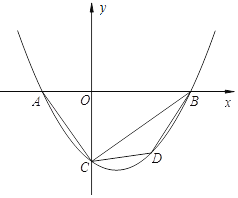
ĄŸÌâÄżĄżÈçÍŒŁŹĆŚÎïÏßyŁœaŁšx+2Ł©Łšx©4Ł©ÓëxÖ᜻ÓÚAŁŹBÁœ”㣏ÓëyÖ᜻ÓÚ”ăCŁŹÇÒĄÏACOŁœĄÏCBOŁź
Łš1Ł©ÇóÏ߶ÎOC”Äł€¶ÈŁ»
Łš2Ł©Èô”ăDÔÚ”ÚËÄÏóÏȚ”ÄĆŚÎïÏßÉÏŁŹÁŹœÓBDĄąCDŁŹÇóĄśBCD”ÄĂæ»ę”ÄŚîŽóÖ”Ł»
Łš3Ł©Èô”ăPÔÚÆœĂæÄÚŁŹ”±ÒÔ”ăAĄąCĄąBĄąPÎȘ¶„”ă”ÄËıßĐÎÊÇÆœĐĐËıßĐÎʱŁŹÖ±œÓĐŽłö”ăP”ÄŚű±êŁź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÔÚÆœĂæÖ±œÇŚű±êÏ”xOyÖĐŁŹœ«Ò»żéșŹÓĐ45ĄăœÇ”ÄÖ±œÇÈęœÇ°ćÈçÍŒ·ĆÖĂŁŹÖ±œÇ¶„”ăC”ÄŚű±êÎȘŁš1ŁŹ0Ł©ŁŹ¶„”ăA”ÄŚű±êÎȘŁš0ŁŹ2Ł©ŁŹ¶„”ăBÇĄșĂÂäÔÚ”ÚÒ»ÏóÏȚ”ÄË«ÇúÏßÉÏŁŹÏÖœ«Ö±œÇÈęœÇ°ćŃŰxÖáŐę·œÏòÆœÒÆŁŹ”±¶„”ăAÇĄșĂÂäÔÚžĂË«ÇúÏßÉÏÊ±ÍŁÖčÔ˶ŻŁŹÔòŽËʱ”ăC”ĶÔÓŠ”ăCĄä”ÄŚű±êÎȘŁšĄĄĄĄŁ©
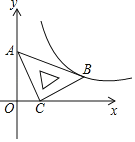
A.Łš![]() ŁŹ0Ł©B.Łš2ŁŹ0Ł©C.Łš
ŁŹ0Ł©B.Łš2ŁŹ0Ł©C.Łš![]() ŁŹ0Ł©D.Łš3ŁŹ0Ł©
ŁŹ0Ł©D.Łš3ŁŹ0Ł©
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹÔÚ·Ž±ÈÀęșŻÊęyŁœ![]() ŁšxŁŸ0Ł©”ÄÍŒÏóÉÏŁŹÓĐ”ăP1ĄąP2ĄąP3ĄąP4ŁŹËüĂÇ”ÄșáŚű±êÒÀŽÎÎȘ1ŁŹ2ŁŹ3ŁŹ4Łź·Ö±đčęŐâĐ©”㌜xÖáÓëyÖá”ÄŽčÏߣŹÍŒÖĐËùččłÉ”ÄÒőÓ°Čż·Ö”ÄĂæ»ęŽÓŚó”œÓÒÒÀŽÎÎȘS1ĄąS2ĄąS3ŁŹÔòS1+S2+S3ŁœŁšĄĄĄĄŁ©
ŁšxŁŸ0Ł©”ÄÍŒÏóÉÏŁŹÓĐ”ăP1ĄąP2ĄąP3ĄąP4ŁŹËüĂÇ”ÄșáŚű±êÒÀŽÎÎȘ1ŁŹ2ŁŹ3ŁŹ4Łź·Ö±đčęŐâĐ©”㌜xÖáÓëyÖá”ÄŽčÏߣŹÍŒÖĐËùččłÉ”ÄÒőÓ°Čż·Ö”ÄĂæ»ęŽÓŚó”œÓÒÒÀŽÎÎȘS1ĄąS2ĄąS3ŁŹÔòS1+S2+S3ŁœŁšĄĄĄĄŁ©
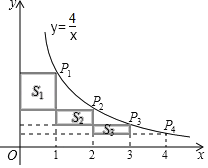
A.2B.2.5C.3D.ÎȚ·šÈ·¶š
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹÒ»¶ÎĆŚÎïÏßy=©xŁšx©5Ł©Łš0ĄÜxĄÜ5Ł©ŁŹŒÇÎȘC1ŁŹËüÓëxÖ᜻ÓÚ”ăOŁŹA1Ł»œ«C1ÈÆ”ăA1ĐęŚȘ180Ąă”ĂC2ŁŹœ»xÖáÓÚ”ăA2Ł»œ«C2ÈÆ”ăA2ĐęŚȘ180Ąă”ĂC3ŁŹœ»xÖáÓÚ”ăA3Ł»ĄÈçŽËœűĐĐÏÂÈ„ŁŹ”Ă”œÒ»Ą°ČšÀËÏߥ±ŁŹÈô”ăPŁš2018ŁŹmŁ©ÔÚŽËĄ°ČšÀËÏߥ±ÉÏŁŹÔòm”ÄÖ”ÎȘ_____Łź
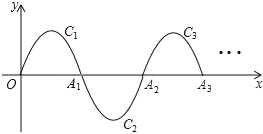
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÒŃÖȘÈçÍŒĄśABCÖĐŁŹÒÔABÎȘÖ±Ÿ¶”ÄĄŃOÓëACŁŹBC”Äœ»”ă·Ö±đÎȘDŁŹEŁź
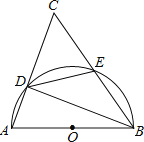
Łš1Ł©ĄÏAŁœ68ĄăŁŹÇóĄÏCED”ÄŽóĐĄ.
Łš2Ł©”±DEŁœBEʱŁŹÖ€ĂśŁșĄśABCÎȘ”ÈŃüÈęœÇĐÎŁź
Č鿎Žđ°žșÍœâÎö>>
°Ù¶ÈÖÂĐĆ - Á·Ï°ČáÁбí - ÊÔÌâÁбí
șț±±ÊĄ»„ÁȘÍű΄·šșÍČ»ÁŒĐĆÏąŸÙ±šÆœÌš | ÍűÉÏÓĐșŠĐĆÏąŸÙ±šŚšÇű | ”çĐĆŐ©ÆŸÙ±šŚšÇű | ÉæÀúÊ·ĐéÎȚÖśÒćÓĐșŠĐĆÏąŸÙ±šŚšÇű | ÉæÆóÇÖÈšŸÙ±šŚšÇű
΄·šșÍČ»ÁŒĐĆÏąŸÙ±š”ç»°Łș027-86699610 ŸÙ±šÓÊÏäŁș58377363@163.com