
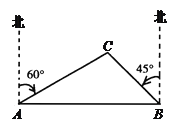
【题目】已知:如图,一艘渔船正在港口A的正东方向40海里的B处进行捕鱼作业,突然接到通知,要该船前往C岛运送一批物资到A港,已知C岛在A港的北偏东60°方向,且在B的北偏西45°方向.问该船从B处出发,以平均每小时20海里的速度行驶,需要多少时间才能把这批物资送到A港(精确到1小时)(该船在C岛停留半个小时)?(![]() ,
,![]() ,
,![]() )
)
【答案】3小时.
【解析】
作CD⊥AB于D点.设CD=x海里,在直角△ACD中,利用x表示出AC,AD,同理表示出BD,BC,根据AB=40即可列出方程求得CD的长,则AC+CB即可求得,然后除以速度即可得到时间.
作CD⊥AB于D点.设CD=x海里,
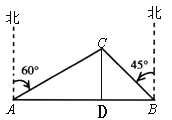
在直角△ACD中,∠CAD=90°-60°=30°,
则AC=2x,AD=![]() x,
x,
在直角△BCD中,∠CBD=45°,
则BD=CD=x,BC=![]() CD=
CD=![]() x,
x,
∵AB=40,即AD+BD=40,
∴![]() x+x=40,
x+x=40,
解得:x=20(![]() -1),
-1),
∴BC=20![]() (
(![]() -1)=20
-1)=20![]() -20
-20![]() ,AC=2x=40(
,AC=2x=40(![]() -1),
-1),
则总路程是:20![]() -20
-20![]() +40(
+40(![]() -1)海里,
-1)海里,
则时间是:![]() (小时).
(小时).
∵该船在C岛停留半个小时,
∴需要3小时能把这批物资送到A港.
考点: 解直角三角形的应用-方向角问题.


科目:初中数学 来源: 题型:
【题目】甲、乙两所医院分别有一男一女共4名医护人员支援湖北武汉抗击疫情.
(1)若从甲、乙两医院支援的医护人员中分别随机选1名,则所选的2名医护人员性别相同的概率是 ;
(2)若从支援的4名医护人员中随机选2名,用列表或画树状图的方法求出这2名医护人员来自同一所医院的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
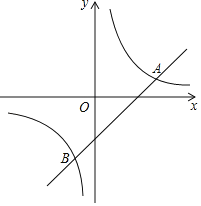
【题目】如图,在平面直角坐标系xOy中,直线y=x﹣2与双曲线y=![]() (k≠0)相交于A,B两点,且点A的横坐标是3.
(k≠0)相交于A,B两点,且点A的横坐标是3.
(1)求k的值;
(2)过点P(0,n)作直线,使直线与x轴平行,直线与直线y=x﹣2交于点M,与双曲线y=![]() (k≠0)交于点N,若点M在N右边,求n的取值范围.
(k≠0)交于点N,若点M在N右边,求n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
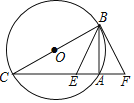
【题目】如图,BC为圆O直径,BF与圆O相切于点B,CF交圆O于A,E为AC上一点,使∠EBA=∠FBA,若EF=6,tan∠F=![]() ,则CE的长为_____.
,则CE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=8,∠BAC,∠ACB的平分线相交于点E,过点E作EF∥BC交AC于点F,则EF的长为( )
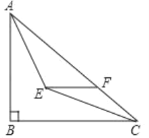
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, AB 是⊙O 的直径,点 C 和点 D 是⊙O 上两点,连接 AC 、CD 、 BD ,若 CA= CD,∠ ACD = 80° ,则∠ CAB =______________.
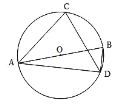
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个工厂需加工生产 550 台某种机器,已知甲工厂每天加工生产的机器台数是乙工厂每天加工 生产的机器台数的 1.5 倍,并且加工生产 240 台这种机器甲工厂需要的时间比乙工厂需要的时间少 4 天
(1)求甲、乙两个工厂每天分别可以加工生产多少台这种机器?
(2)若甲工厂每天加工的生产成本是 3 万元,乙工厂每天加工生产的成本是 2.4 万元,要使得加工生 产这批机器的总成本不得高于 60 万元,至少应该安排甲工厂生产多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=kx+b过x轴上的点A(2,0),且与抛物线![]() 交于B,C两点,点B坐标为(1,1).
交于B,C两点,点B坐标为(1,1).
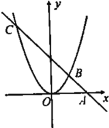
(1)求直线与抛物线对应的函数表达式;
(2)当![]() 时,请根据图象写出自变量x的取值范围;
时,请根据图象写出自变量x的取值范围;
(3)抛物线上是否存在一点D,使![]() ?若存在,求出D点坐标;若不存在,请说明理由
?若存在,求出D点坐标;若不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图抛物线y=ax2+bx+![]() 与y轴交于点A,与x轴交于点B、点C.连接AB,以AB为边向右作平行四边形ABDE,点E落在抛物线上,点D落在x轴上,若抛物线的对称轴恰好经过点D,且∠ABD=60°,则这条抛物线的解析式为( )
与y轴交于点A,与x轴交于点B、点C.连接AB,以AB为边向右作平行四边形ABDE,点E落在抛物线上,点D落在x轴上,若抛物线的对称轴恰好经过点D,且∠ABD=60°,则这条抛物线的解析式为( )
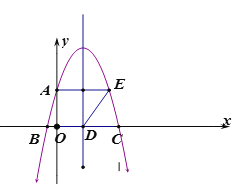
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com