
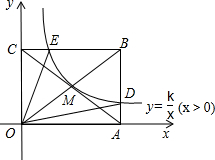
 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过矩形OABC对角线的交点M,分别与AB,BC交于点D,E,若四边形ODBE的面积为6,则△OAD的面积为( )
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过矩形OABC对角线的交点M,分别与AB,BC交于点D,E,若四边形ODBE的面积为6,则△OAD的面积为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据题意,可以求得k的值,从而可以求得△OAD的面积,本题得以解决.
解答 解:设OA=a,OC=b,
∵反比例函数y=$\frac{k}{x}$(x>0)的图象经过矩形OABC对角线的交点M,
∴点M($\frac{a}{2},\frac{b}{2}$),
∴$\frac{b}{2}=\frac{k}{\frac{a}{2}}$,得ab=4k,
又∵四边形ODBE的面积为6,△COE的面积与△OAD的面积都是$\frac{k}{2}$,
∴6+$\frac{k}{2}+\frac{k}{2}$=ab,
解得,k=2,
∴△OAD的面积是1,
故选A.
点评 本题考查反比例函数系数k的几何意义、反比例函数图象上点的坐标特征,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.


科目:初中数学 来源: 题型:填空题
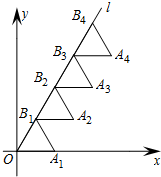 如图放置的△OB1A1,△B1B2A2,△B2B3A3,…,都是边长为2的等边三角形,边OA1在x轴上,且点O,B1,B2,B3,…,都在同一直线上,则A2015的坐标是(2016,2014$\sqrt{3}$).
如图放置的△OB1A1,△B1B2A2,△B2B3A3,…,都是边长为2的等边三角形,边OA1在x轴上,且点O,B1,B2,B3,…,都在同一直线上,则A2015的坐标是(2016,2014$\sqrt{3}$).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 原式=(x-3)-(2-x)=2x-1 | B. | 原式=(3-x)-(x-2)=5-2x | ||
| C. | 原式=(3-x)-(2-x)=1 | D. | 原式=(x-3)-(x-2)=-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ②③ | D. | ③ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (2,3) | B. | (-2,-3) | C. | (-3,2) | D. | (3,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com