
����Ŀ����һ��ֱ����������A��B��C����������ij��Ѳ����A��������ֱ�����پ�B ��ʻ��C����ִ�к�Ѳ�������մﵽC������ú�Ѳ����ʻx��h������B�۵ľ���Ϊy��km����y��x�ĺ�����ϵ��ͼ��ʾ�� 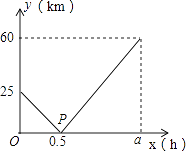
��1����գ�A��C���ۿڼ�ľ���Ϊkm��a=��
��2����y��x�ĺ�����ϵʽ���������ͼ�е�P����������ʾ��ʵ�����壻
��3����B����һ����Ϸ����źŵ��źŷ���̨��������źŸ��ǰ뾶Ϊ15km����ú�Ѳ���ܽ��ܵ����źŵ�ʱ���ж��
���𰸡�
��1��85��1.7h
��2���⣺��0��x��0.5ʱ����y��x�ĺ�����ϵʽΪ��y=kx+b��
�ߺ���ͼ���㣨0��25������0.5��0����
�� ![]() ��
��
��� ![]() ��
��
���ԣ�y=��50x+25��
��0.5��x��1.7ʱ����y��x�ĺ�����ϵʽΪ��y=mx+n��
�ߺ���ͼ���㣨0.5��0������1.7��60����
�� ![]() ��
��
��� ![]() ��
��
���ԣ�y=50x��25��
��3���⣺�ɩ�50x+25=15��
���x=0.2��
��50x��25=15��
���x=0.8��
���ԣ��ú�Ѳ���ܽ��ܵ����źŵ�ʱ��Ϊ��0.6h
���������⣺��1����ͼ��֪��A��B�ۿڼ�ľ���Ϊ25��B��C�ۿڼ�ľ���Ϊ60�� ���ԣ�A��C�ۿڼ�ľ���Ϊ��25+60=85km��
��Ѳ�����ٶ�Ϊ��25��0.5=50km/h��
��a=85��50=1.7h��
���Դ��ǣ�85��1.7h��


 ��ĩ��ϰ���ϵ�д�
��ĩ��ϰ���ϵ�д� ����ѧ�䵥Ԫ������ĩר����100��ϵ�д�
����ѧ�䵥Ԫ������ĩר����100��ϵ�д� �Ƹ�360�ȶ����ܾ�ϵ�д�
�Ƹ�360�ȶ����ܾ�ϵ�д� ���⿼����Ԫ���Ծ�ϵ�д�
���⿼����Ԫ���Ծ�ϵ�д� ��У���˳�̾�ϵ�д�
��У���˳�̾�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC=5��BC=6��ADΪBC���ϵĸߣ�����A��AE��BC������D��DE��AC��AE��DE���ڵ�E��AB��DE���ڵ�F������BE�����ı���AEBD������� 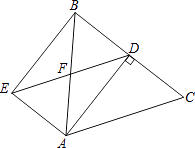
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����P��3a��a���Ƿ���������y= ![]() ��k��0�����O��һ�����㣬ͼ����Ӱ���ֵ����Ϊ10�У����������Ľ���ʽΪ�� ��
��k��0�����O��һ�����㣬ͼ����Ӱ���ֵ����Ϊ10�У����������Ľ���ʽΪ�� ��
A.y= ![]()
B.y= ![]()
C.y= ![]()
D.y= ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij�ִ�������һб��AB�����¶�Ϊi=1��2������A���ĸ�ACΪ4m��B��C��ͬһˮƽ�����ϣ�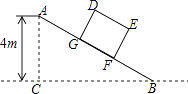
��1����б��AB��ˮƽ����BC��
��2������DEFGΪ���������IJ���ͼ������DE=2.5m��EF=2m�����û�����б���������ͣ���BF=3.5mʱ�����D�����ĸߣ�������������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У���E��F��G��H�ֱ��ڱ�AB��BC��CD��DA�ϣ���P�ھ���ABCD�ڣ���AB=4cm��BC=6cm��AE=CG=3cm��BF=DH=4cm���ı���AEPH�����Ϊ5cm2 �� ���ı���PFCG�����Ϊcm2 �� 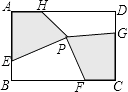
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�Rt��ABC�Ķ���A��C�ֱ���y�ᣬx���ϣ���ACB=90�㣬OA= ![]() ��������y=ax2��ax��a������B��2��
��������y=ax2��ax��a������B��2�� ![]() ������y�ύ�ڵ�D��
������y�ύ�ڵ�D��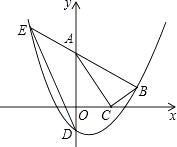
��1���������ߵı���ʽ��
��2����B����ֱ��AC�ĶԳƵ��Ƿ����������ϣ���˵�����ɣ�
��3���ӳ�BA���������ڵ�E������ED����˵��ED��AC�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��һ����Ϊ2a����Ϊ2b�ij�����������a��b��Ϊ��������a��b������ͼ�������ü������ȷֳ��Ŀ���ͬС�����Σ�Ȼ��ͼ2��ʽƴ��һ������������
��1������Ϊͼ2�д������εı߳�Ϊ a+b ��С����������Ӱ�������ı߳�Ϊ �����ú�a��b�Ĵ���ʽ��ʾ��
��2����ϸ�۲�ͼ2������д��������������ʽ����a+b��2����a-b��2��ab����ʾ��ͼ�����֮�����ȹ�ϵ����ѡȡ�ʺ�a��b����ֵ������֤��
��3����֪a+b=7��ab=6�������ʽ��a-b����ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�Ķ��κ���y=ax2+bx+c��ͼ���㣨��2��y1��������1��y2������1��0������y1��0��y2 �� �������½��ۣ�
��abc��0����a+3b+2c��0���۶����Ա���x������һ��ȡֵ������ ![]() x2+x�ݩ�
x2+x�ݩ� ![]() �����ک�2��x����1�д���һ��ʵ��x0 �� ʹ��x0=��
�����ک�2��x����1�д���һ��ʵ��x0 �� ʹ��x0=�� ![]() ��
��
���н��۴������ ��ֻ��д��ţ���
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com