
分析 首先设函数解析式为y=kx+b,根据图象与y轴交于点(0,6)可得b=6,然后再根据图象与x轴、y轴围成的三角形的面积是12可得函数与x轴的交点为(4,0)或(-4,0),再分别计算出k的值,进而可得函数解析式.
解答 解:设函数解析式为y=kx+b,
∵图象与y轴交于点(0,6),
∴b=6,
∵图象与x轴、y轴围成的三角形的面积是12,
∴函数与x轴的交点为(4,0)或(-4,0),
①当与x轴的交点为(4,0)时,0=4k+6,
解得k=-$\frac{3}{2}$,
∴函数解析式为y=-$\frac{3}{2}$x+6;
②当与x轴的交点为(-4,0)时,0=-4k+6,
解得k=$\frac{3}{2}$,
∴函数解析式为y=$\frac{3}{2}$x+6.
点评 此题主要考查了待定系数法求一次函数解析式,关键是掌握凡是函数经过的点必能满足解析式,注意分类讨论,不能漏解.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:选择题
 如图,在矩形ABCD中,AE⊥BD交BC于E,垂足为F,BG平分∠ABD交AE于H,GP∥BD交AE于P,下列结论:
如图,在矩形ABCD中,AE⊥BD交BC于E,垂足为F,BG平分∠ABD交AE于H,GP∥BD交AE于P,下列结论:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
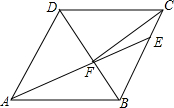 如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC,BD于点E,F,CE=2,连接CF,以下结论::①△ABF≌△CBF;②点E到AB的距离是2$\sqrt{3}$;③CF=5;④△CEF的面积为$\frac{6}{5}$$\sqrt{3}$.其中一定成立的是①②④(把所有正确结论的序号都填在横线上).
如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC,BD于点E,F,CE=2,连接CF,以下结论::①△ABF≌△CBF;②点E到AB的距离是2$\sqrt{3}$;③CF=5;④△CEF的面积为$\frac{6}{5}$$\sqrt{3}$.其中一定成立的是①②④(把所有正确结论的序号都填在横线上).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
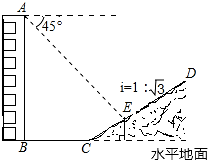 如图,一楼房AB后有一假山,其坡度为i=1:$\sqrt{3}$,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=26米,与亭子距离CE=18米,小丽从楼房顶测得E点的俯角为45°.(注:坡度i是指坡面的铅直高度与水平宽度的比)
如图,一楼房AB后有一假山,其坡度为i=1:$\sqrt{3}$,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=26米,与亭子距离CE=18米,小丽从楼房顶测得E点的俯角为45°.(注:坡度i是指坡面的铅直高度与水平宽度的比)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com