Question

半径为2cm的与⊙O边长为2cm的正方形ABCD在水平直线l的同侧，⊙O与l相切于点F，DC在l上．

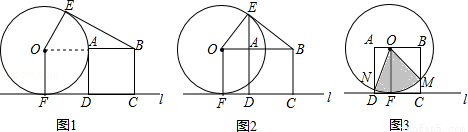
（1）过点B作的一条切线BE，E为切点．

①填空：如图1，当点A在⊙O上时，∠EBA的度数是　    　；

②如图2，当E，A，D三点在同一直线上时，求线段OA的长；

（2）以正方形ABCD的边AD与OF重合的位置为初始位置，向左移动正方形（图3），至边BC与OF重合时结束移动，M，N分别是边BC，AD与⊙O的公共点，求扇形MON的面积的范围．

 

Answer 1

【答案】

解：（1）①30°。

②

 （2）

【解析】

试题分析：（1）①根据切线的性质以及直角三角形的性质得出∠EBA的度数即可：

∵半径为2cm的与⊙O边长为2cm的正方形ABCD在水平直线l的同侧，当点A在⊙O上时，过点B作的一条切线BE，E为切点，

∴OB=4，EO=2，∠OEB=90°。       

∴∠EBA的度数是：30°。

②利用切线的性质以及矩形的性质和相似三角形的判定和性质得出，进而求出OA即可。

如图2，

∵直线l与⊙O相切于点F，∴∠OFD=90°。

∵正方形ADCB中，∠ADC=90°，∴OF∥AD。

∵OF=AD=2，∴四边形OFDA为平行四边形。

∵∠OFD=90°，∴平行四边形OFDA为矩形。∴DA⊥AO。

∵正方形ABCD中，DA⊥AB，O、A、B三点在同一条直线上，∴EA⊥OB。

∵∠OEB=∠AOE，∴△EOA∽△BOE。

∴，即，解得：。

∵OA＞0，∴。

（2）设∠MON=n°，得出，进而利用函数增减性分析①当N，M，A分别与D，B，O重合时，MN最大，②当MN=DC=2时，MN最小，分别求出即可。

如图3，设∠MON=n°，（cm²）。

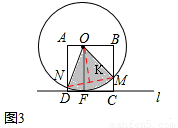
∴S随n的增大而增大，当∠MON取最大值时，S_扇形MON最大，当∠MON取最小值时，S_扇形MON最小。    

过O点作OK⊥MN于K，∴∠MON=2∠NOK，MN=2NK。

在Rt△ONK中，，

∴∠NOK随NK的增大而增大。

∴∠MON随MN的增大而增大。

∴当MN最大时∠MON最大，当MN最小时∠MON最小。

①当N，M，A分别与D，B，O重合时，MN最大，

此时，MN=BD，∠MON=∠BOD=90°，（cm²）。

②当MN=DC=2时，MN最小，

此时，ON=MN=OM。∴∠NOM=60°。（cm²）。

∴。